परिभाषा: एक समीकरण एक चर के साथ 
समानता है एक चर के साथ 
, जो सामान्य रूप में इस तरह लिखा है: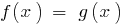 
परिभाषा: एक जड़ (या rozvyazka) समीकरण कहा जाता है चर के मूल्य बनाता है कि समीकरण सच्चे संख्यात्मक समानता है ।
Razvesti समीकरण खोजने का मतलब है अपने सभी जड़ों (इंटरचेंज) या दिखाने के लिए कि वे नहीं कर रहे हैं.
क्षेत्र की स्वीकार्य मूल्यों (odz) समीकरण
परिभाषा: क्षेत्र की स्वीकार्य मूल्यों (रेंज की परिभाषा) के समीकरण — समग्र के लिए गुंजाइश कार्यों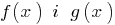 
में खड़े छोड़ दिया और सही भागों के समीकरण है.
क्षेत्र खोजने के लिए स्वीकार्य मूल्यों (odz)
उदाहरण
सेट समीकरण: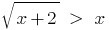 
DHS: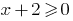 
यानी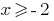 
, के रूप में समारोह के डोमेन 
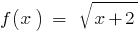स्थिति से निर्धारित होता है 
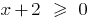, और समारोह के डोमेन 
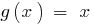सेट है के सभी वास्तविक संख्या है.
समीकरण — जांच
अगर हर रूट के समीकरण की जड़ है दूसरा समीकरण, दूसरा समीकरण कहा जाता है का परिणाम पहले समीकरणहै ।
यदि वैधता की समानता का अर्थ है शुद्धता के साथ निम्न में से प्रत्येक के, फिर, adejumo समीकरण का एक परिणाम है
इसलिए, जब का उपयोग कर समीकरण और प्रभाव सत्यापन की जड़ों में प्रतिस्थापन द्वारा मूल समीकरण का एक हिस्सा है समाधान.
उदाहरण 1
Razvesti समीकरण: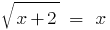 
समाधान:
चलो का निर्माण दोनों भागों समीकरण के एक वर्ग में:
;
;
;
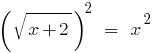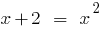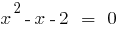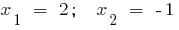है ।
क्या एक पृष्ठभूमि की जाँच करें.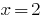 
— जड़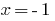 
है जड़ है.
जवाब: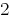 
.
बराबर समीकरण
परिभाषा: समकक्ष (बराबर) समीकरण — दो समीकरण, जो कई के लिए सरकारी विभाग एक ही परिणाम है, कि है, हर समाधान के समीकरण है rozvyazka दूसरे, और इसके विपरीत.
कुछ प्रमेयों के बारे में समान रूप से प्रभावी या तो समीकरण
प्रमेय 1: अगर एक समीकरण का हिस्सा स्थानांतरित करने के लिए किसी अन्य भाग के लिए शर्तों के साथ विपरीत संकेत है, हम एक समीकरण के बराबर करने के लिए दिए गए (पर किसी भी सेट).
प्रमेय 2: यदि दोनों भागों के समीकरण गुणा या विभाजित एक ही नंबर के द्वारा नहीं के बराबर शून्य करने के लिए (या करने के लिए एक और एक ही है कि समारोह परिभाषित किया गया है, और नहीं शून्य के बराबर पर IDS के दिए गए समीकरण), हम समीकरण के बराबर दी.
प्रमेय 3: अगर दोनों समीकरण के कुछ हिस्सों को 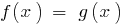लेने के लिए एक बढ़ती (या अवरोही) समारोह 
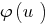और नहीं vdbase संकुचन आईडी के दिए गए समीकरण 
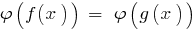के बराबर हो जाएगा एक दिया ( DHS).
परिणाम के प्रमेयों के बारे में समान रूप से प्रभावी या तो समीकरण
परिणाम: क्योंकि समारोह है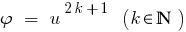 
monotonically बढ़ाने,तो
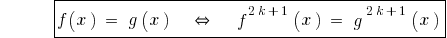है ।
प्रस्तुति में दोनों के समीकरण के कुछ हिस्सों में अजीब प्राकृतिक डिग्री के परिणामस्वरूप समीकरण के बराबर है ।
परिणाम: क्योंकि समारोह है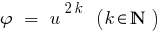 
monotonically बढ़ाने तभी 
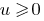है,जब मामले में दोनों भागों के समीकरण newmn, द्वारा उठाने के दोनों भागों के लिए भी प्राकृतिक डिग्री के परिणामस्वरूप समीकरण के बराबर है ।