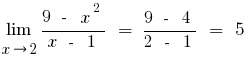
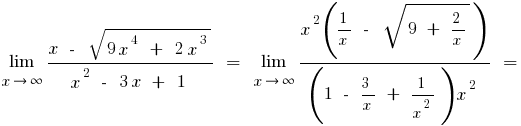
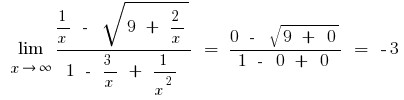
एक) की कोशिश करने के लिए विघटित अंश और सर्वनाम.
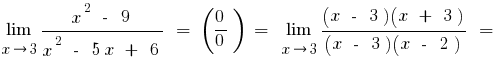
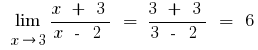
ख) यदि अंश में या भाजक के अभिव्यक्ति के साथ वर्ग या घन रूट, गुणा है कि अमेरिका और भाजक द्वारा उचित अभिव्यक्ति से छुटकारा पाने के लिए सेट की जड़ों (कभी कभी प्रशासित को बदलने के लिए अभिव्यक्ति की जड़ का अर्थ है नए चर)
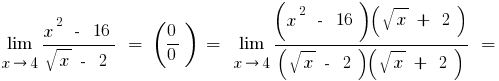
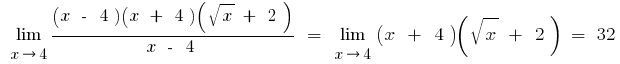
C) यदि के हस्ताक्षर के तहत सीमित कर रहे हैं या त्रिकोणमितीय, उलटा त्रिकोणमितीय कार्यों, इन सीमाओं को कम करने के लिए सीमाओं के बकाया पहली

या अपनी विविधताओं



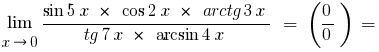
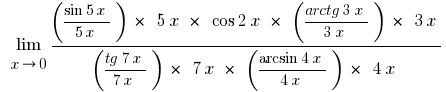
कम अंश और हर चर बाहर खड़ा है कि, यह देखते हुए कि 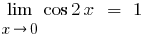 , और दिया जाएगा persu बकाया सीमा और अपनी विविधताओं, हम प्राप्त
, और दिया जाएगा persu बकाया सीमा और अपनी विविधताओं, हम प्राप्त 
- का उपयोग निरंतरता के समारोह में
 , हम कोशिश करने के लिए स्थानापन्न मूल्यों
, हम कोशिश करने के लिए स्थानापन्न मूल्यों  में समारोह
में समारोह 
- यदि आप गणना के लिए एक सीमा से कम
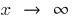 है, तो कोशिश अंश में और सर्वनाम के लिए कोष्ठक बनाने के सर्वोच्च डिग्री की अज्ञात
है, तो कोशिश अंश में और सर्वनाम के लिए कोष्ठक बनाने के सर्वोच्च डिग्री की अज्ञात - यदि परिणाम के लुक
 प्राप्त अभिव्यक्ति के प्रकार
प्राप्त अभिव्यक्ति के प्रकार 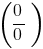 ,
,

 , हम कोशिश करने के लिए स्थानापन्न मूल्यों
, हम कोशिश करने के लिए स्थानापन्न मूल्यों  में समारोह
में समारोह 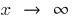 है, तो कोशिश अंश में और सर्वनाम के लिए कोष्ठक बनाने के सर्वोच्च डिग्री की अज्ञात
है, तो कोशिश अंश में और सर्वनाम के लिए कोष्ठक बनाने के सर्वोच्च डिग्री की अज्ञात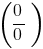 ,
,