परिभाषा: एक बहुपद की एक चर  है एक बहुपद के रूप
है एक बहुपद के रूप 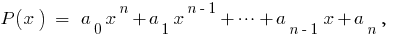 में जहां
में जहां 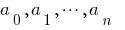 संख्यात्मक गुणांकों.
संख्यात्मक गुणांकों.
परिभाषा: यदि 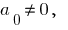 यह बहुपद कहा जाता है बहुपद
यह बहुपद कहा जाता है बहुपद  की डिग्री करने के लिए अपेक्षाकृत चर
की डिग्री करने के लिए अपेक्षाकृत चर  .
.
सदस्य 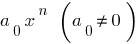 कहा जाता है के एक वरिष्ठ सदस्य के बहुपद
कहा जाता है के एक वरिष्ठ सदस्य के बहुपद 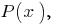 एक
एक 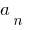 — यह नि: शुल्क सदस्यहै ।
— यह नि: शुल्क सदस्यहै ।
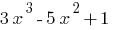 — बहुपद की तीसरी डिग्री ।
— बहुपद की तीसरी डिग्री ।
हूबहू बराबर polynomials में एक चर
परिभाषा: दो polynomials कर रहे हैं कहा जाता है के बराबरहै अगर वे समान मूल्यों के सभी मूल्यों के लिए चर.
गुण समान के साथ समानता के polynomials में एक चर
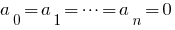
- यदि बहुपद
 है identically शून्य के बराबर है (यानी शून्य मूल्यों पर सभी मूल्यों
है identically शून्य के बराबर है (यानी शून्य मूल्यों पर सभी मूल्यों  ), तो सभी के अपने गुणांक शून्य के बराबर हैं ।
), तो सभी के अपने गुणांक शून्य के बराबर हैं । - अगर दो बहुपद
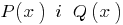 हूबहू बराबर करने के लिए (यानी, एक ही अधिग्रहण मूल्य पर सभी मूल्यों
हूबहू बराबर करने के लिए (यानी, एक ही अधिग्रहण मूल्य पर सभी मूल्यों  ), तो वे मेल (यानी, उनकी डिग्री के बराबर हैं और गुणांक के बराबर शक्तियों के बराबर).
), तो वे मेल (यानी, उनकी डिग्री के बराबर हैं और गुणांक के बराबर शक्तियों के बराबर).
विभाजन के बहुपद बहुपद द्वारा
परिभाषा: अगर दो polynomials 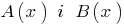 यह संभव है खोजने के लिए एक बहुपद
यह संभव है खोजने के लिए एक बहुपद 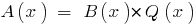 उस
उस 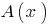 में बांटा गया है
में बांटा गया है  .
.
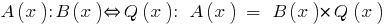
उदाहरण
के बाद से 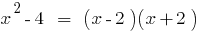 , बहुपद
, बहुपद 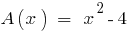 है विभाज्य द्वारा बहुपद
है विभाज्य द्वारा बहुपद 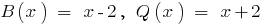
विभाजन के बहुपद द्वारा बहुपद एस स्टेसी
परिभाषा: एक बहुपद 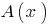 से विभाजित है बहुपद
से विभाजित है बहुपद  एस स्टेसी, यदि आप कर सकते हैं की एक जोड़ी मिल polynomials
एस स्टेसी, यदि आप कर सकते हैं की एक जोड़ी मिल polynomials 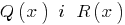 ,
, 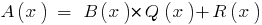 और डिग्री के शेष के
और डिग्री के शेष के 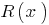 छोटे डिग्री
छोटे डिग्री  है ।
है ।
यदि शेष 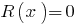 है, तो इस बहुपद
है, तो इस बहुपद 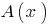 है विभाज्य द्वारा बहुपद
है विभाज्य द्वारा बहुपद  एक शेष बिना)
एक शेष बिना)
उदाहरण
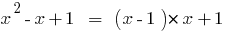
,
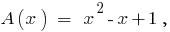
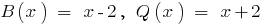
विभाजन के बहुपद द्वारा बहुपद "क्षेत्र"
शासन के विभाजन के polynomials में एक चर
- जगह करने के लिए सदस्यों के polynomials के साथ उतरते exponents के चर.
- साझा करने के लिए एक वरिष्ठ सदस्य के लाभांश पर वरिष्ठ सदस्य के विभक्त है ।
- परिणाम से गुणा किया जाता है भाजक और घटाना इस उत्पाद से लाभांश का.
- के साथ अंतर को प्राप्त एक ही आपरेशन प्रदर्शन: यह विभाजित वरिष्ठ सदस्य वरिष्ठ सदस्य के साथ विभक्त और परिणाम फिर से गुणा भाजक, और इतने पर । इस प्रक्रिया को जारी रखने के लिए दे जब तक मैं संतुलन शून्य करने के लिए (यदि एक बहुपद द्वारा विभाजित एक) या के रूप में लंबे समय के रूप में संतुलन नहीं मिलता है बहुपद की डिग्री है, कम से कम डिग्री के भाजक है ।
प्रमेय निरंतर
शेष विभाजित करने के लिए बहुपद  पर doclen
पर doclen 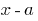 बराबर
बराबर 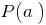
परिणाम: अगर 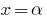 एक रूट के बहुपद
एक रूट के बहुपद  (यानी,
(यानी, 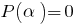 ) है, तो इस बहुपद बांटा गया है
) है, तो इस बहुपद बांटा गया है 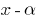 .
.
उदाहरण
शेष विभाजित करने के लिए बहुपद 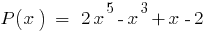 पर doclen
पर doclen 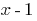 बराबर
बराबर 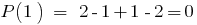 है, कि है
है, कि है  में विभाजित
में विभाजित 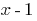 एक शेष बिना.
एक शेष बिना.
विभाजन  में
में 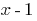 "क्षेत्र" या होर्नर की योजना है, हम प्राप्त:
"क्षेत्र" या होर्नर की योजना है, हम प्राप्त: 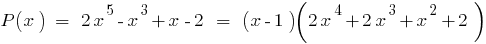

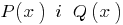 हूबहू बराबर करने के लिए (यानी, एक ही अधिग्रहण मूल्य पर सभी मूल्यों
हूबहू बराबर करने के लिए (यानी, एक ही अधिग्रहण मूल्य पर सभी मूल्यों