Definition: a Polynomial of one variable 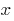 is a polynomial of the form
is a polynomial of the form 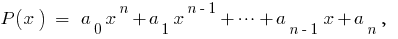 where the
where the 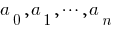 numerical coefficients.
numerical coefficients.
Definition: If 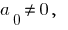 this polynomial is called the polynomial
this polynomial is called the polynomial 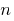 of the first degree relatively variable
of the first degree relatively variable 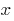 .
.
Member 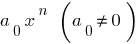 called a senior member of the polynomial
called a senior member of the polynomial 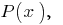 a
a 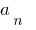 — it free member.
— it free member.
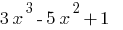 — the polynomial of the third degree.
— the polynomial of the third degree.
Identically equal polynomials in one variable
Definition: Two polynomials are called equalif they take equal values for all values of the variable.
Properties identical with equality of polynomials in one variable
- If the polynomial
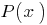 is identically equal to zero (i.e. has zero values at all values
is identically equal to zero (i.e. has zero values at all values 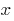 ), then all of its coefficients are equal to zero.
), then all of its coefficients are equal to zero. - If two polynomial
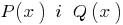 identically equal to (i.e., acquire the same value at all values
identically equal to (i.e., acquire the same value at all values 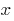 ), then they coincide (i.e., their degrees are equal and the coefficients of equal powers of equal).
), then they coincide (i.e., their degrees are equal and the coefficients of equal powers of equal).
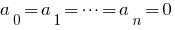
Division of polynomial by polynomial
Definition: If two polynomials 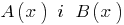 it is possible to find a polynomial
it is possible to find a polynomial 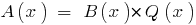 that
that 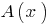 is divided into
is divided into 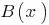 .
.
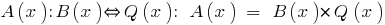
Example
Since 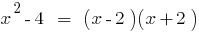 , the polynomial
, the polynomial 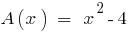 is divisible by the polynomial
is divisible by the polynomial 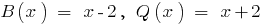
The division of the polynomial by the polynomial s Stacey
Definition: a Polynomial 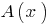 is divided by the polynomial
is divided by the polynomial 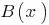 s Stacey, if you can find a pair of polynomials
s Stacey, if you can find a pair of polynomials 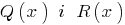 ,
, 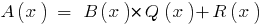 and the degree of the remainder of
and the degree of the remainder of 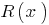 smaller degree
smaller degree 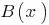 .
.
If the remainder 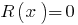 , then the polynomial
, then the polynomial 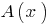 is divisible by the polynomial
is divisible by the polynomial 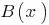 without a remainder)
without a remainder)
Example
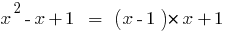
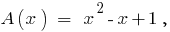
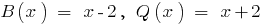
The division of the polynomial by the polynomial "area"
The rule of division of polynomials in one variable
- To place the members of the polynomials with descending exponents of the variable.
- To share a senior member of the dividend on the senior member of the divider.
- The result is multiplied by the divisor and subtract this product from the dividend.
- With the obtained difference perform the same operation: divide it senior member the senior member of the divider and the result again multiplied by the divisor, and so on. This process continue to give until I get the balance to zero (if one polynomial divided by another) or as long as the balance does not get the polynomial degree is less than degree of divisor.
Theorem Continuous
The remainder of dividing the polynomial 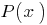 on doclen
on doclen 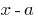 equal
equal 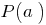
Corollary: If 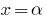 is a root of the polynomial
is a root of the polynomial 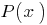 (i.e.,
(i.e., 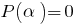 ), then this polynomial is divided
), then this polynomial is divided 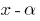 .
.
Example
The remainder of dividing the polynomial 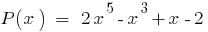 on doclen
on doclen 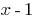 equal
equal 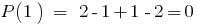 , that is
, that is 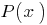 divided into
divided into 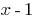 without a remainder.
without a remainder.
Dividing 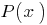 into
into 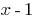 "area" or Horner's scheme, we get:
"area" or Horner's scheme, we get: 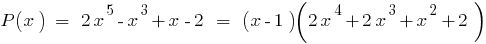

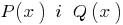 identically equal to (i.e., acquire the same value at all values
identically equal to (i.e., acquire the same value at all values