The definition of a Prime number
Definition: a Natural number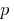 
is called simpleif it has only two positive divisors — the number itself 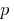and 1.
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, ... — the Prime numbers.
Prime numbers are infinitely many.
The definition of composite numbers
Definition: a Natural number is called compositeif it has more than two positive divisors.
6, 15, 130, ... are composite numbers.
1 is neither Prime number nor composite.
Properties of Prime factors of natural numbers
- Any natural number (greater than unity) or is divided by this Prime number
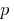, or is coprime with it. - If the product of several factors is divisible by a Prime number 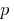, then at least one of the factors is divisible by .
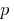- The smallest Prime divisor of a composite number
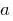not to 
.
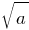.The main theorem of the theory of divisibility
Theorem: Any natural number greater than unity, can be decomposed into the product of primes, and this decomposition is unique up the order of the multiplicands.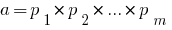
where 
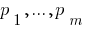are all Prime numbers.
The theorem on division with Stacey
Theorem: For any pair of numbers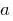 
and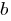 
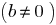there is, and only one pair of integers 
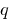and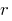 
such that 
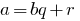, where 
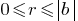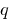( is the incomplete quotient of 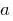at 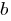, 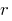— modulo 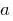on 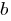).
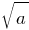