Прості і складені числа, прості дільники

Означення простого числа

Означення: Натуральне число 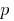називається простим, якщо в нього тільки два натуральних дільники — саме число 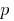і -1.

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, ... — прості числа.

Простих чисел нескінченно багато.

Означення складеного числа

Означення: Натуральне число називається складеним, якщо воно має більше двох натуральних дільників.

6, 15, 130, ... — складені числа.

1 не є ні простим числом, ні складеним.

Властивості простих дільників натуральних чисел

1. Будь-яке натуральне число (більше за одиницю) або ділиться на дане просте число 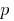, або є взаємно простим з ним.
2. Якщо добуток декількох співмножників ділиться на просте число 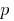, то принаймні один із співмножників ділиться на .
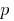3. Найменший простий дільник складеного числа не перевищеє .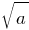

Основна теорема теорії подільності

Теорема: Будь-яке натуральне число, більше за одиницю, можна розкласти в добуток простих чисел, причому цей розклад єдиний з точністю до порядку співмножників.
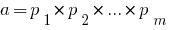, де 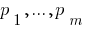— прості числа.

Теорема про ділення з остачею

Теорема: Для будь-якої пари чисел і 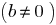існує, і причому єдина, пара цілих чисел 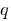і 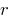, таких, що 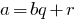, де 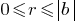( 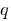— неповна частка від ділення на , 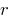— остача від ділення на ).
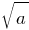