Схема розвязування рівнянь, заміна змінних

Розвязування рівнянь за допомогою рівнянь-наслідків

1. Перетворення, що гарантують збереження правильної рівності
2. Перевірка коренів підстановкою в початкове рівняння

Розвязування рівнянь за допомогою рівносильних перетворень

1. Урахувати ОДЗ правильну рівність при прямих і зворотних перетвореннях
2. Зберігати на ОДЗ правильну рівність при прямих і зворотних перетвореннях

Розвязування рівнянь. Заміна змінних

Якщо до рівняння змінна входить в одному і тому самому вигляді, то зручно відповідний вираз зі змінною позначити однією буквою (новою змінною).

Приклад 1.

Розвяжіть рівняння: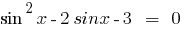

Розвязання.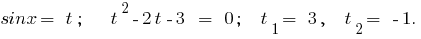

1. При 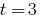рівняння 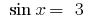коренів не має, оскільки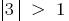

2. При 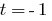маємо 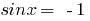, тоді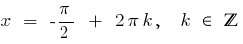

Відповідь: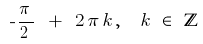

Приклад 2.

Розвяжіть рівняння: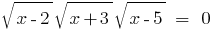

Розвязання. Оскільки під знаком кореня парного степеня можуть стояти тільки невідємні вирази, то область допустимих значень (ОДЗ) заданого рівняння задається системою 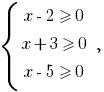розвязком якої є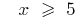

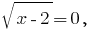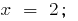
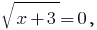Добуток дорівнює нулю тоді і тільки тоді, коли один із множників дорівнює нулю, а всі інші множники існують: при 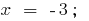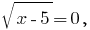при при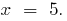

Значення 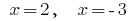не входить до ОДЗ заданого рівняння, отже, вони не є коренями заданого рівняння.

Значення 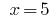входить до ОДЗ, отже, 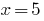є коренем заданого рівняння.

Відповідь: