Системи лінійних рівнянь

Поняття системи та її розвязків

Означення: Лінійні рівняння з двома змінними — це рівняння типу 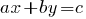, де  і — змінні, 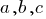— задані числа, для рівняння.

Розв’язком рівняння з двома змінними називається пара значень змінних, яка перетворює рівняння в правильну числову рівність. Ця пара значень змінних називається розв'язком рівняння.

Якщо два невідомі значення зв’язані не одним, а двома рівняннями, то ці рівняння — система лінійних рівнянь з двома змінними.

Розв'язком системи рівнянь з двома змінними називається пара чисел, при яких кожне рівняння системи перетворюється на правильну числову рівність.

Системи лінійних рівнянь з двома змінними можна розв’язати трьома способами:

1. Графічнии спосіб розвязування систем лінійних рівнянь — в одній системі координат будуються графіки двох рівнянь, і координати точки перетину графіків відповідають кореням рівнянь. Найбільш наочний спосіб, але має й найбільші похибки при обчисленнях, оскільки точність визначення координат точки залежить від масштабу зображення. Особливо складним є розв’язування систем, коли коефіцієнти або корені рівнянь — дробові числа.
2. Спосіб підстановки — найбільш універсальний з усіх способів розв’язування лінійних рівнянь з двома змінними. Він використовується практично для всіх типів систем рівнянь.  Спосіб підстановки полягає в тому, що з кожного рівняння одне з невідомих виражається через друге невідоме, і так доти, доки не одержимо результуюче рівняння, у якому буде лише одне невідоме.
3. Спосіб алгебраїчного додавання часто використовується тоді, коли коефіцієнти при одному з невідомих чисельно рівні або їх можна звести до однакової числової величини в рівносильному рівнянні без складних обчислень. Спосіб алгебраїчного додавання полягає в одержанні рівносильного рівняння з одного із даних лінійних рівнянь. Додаючи два рівняння здійснюємо перехід до одного рівняння з одним невідомим.

Розв'язування систем лінійних рівнянь

Графічний спосіб розв'язування систем лінійних рівнянь

Приклад: Розвяжіть рівняння: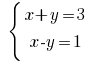

Розвязування:

Будуємо графіки на площині: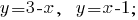  

Побудувавши графіки систем лінійних рівнянь, побачимо, що графіки перетинаються в точці А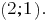 

Відповідь: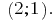

Спосіб підстановки для розв'язування систем лінійних рівнянь

Приклад: Розвяжіть рівняння: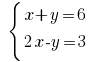

Розв'зування:

З першого рівняння виражаємо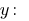

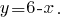
А одержаний вираз підставляємо в друге рівняння системи:

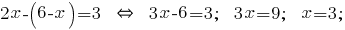
Одержане значення підставляємо у вираз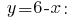

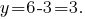
Відповідь: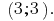

Спосіб додавання для розв'язування систем лінійних рівнянь

Приклад: Розвяжіть рівняння: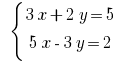

Розвязання:

Маємо позбутись змінної 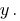Множимо почленно перше рівняння системи на 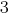, а друге – на .

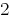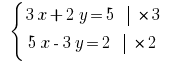
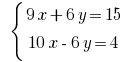
Почленно додаємо лінійні рівняння і одержуємо: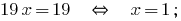

Знаходимо значення з першого рівняння системи: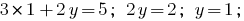

Відповідь: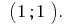

Зауваження: В методі додавання можна множити не тільки на додатні числа, а і на від'ємні.

Також Ви можете ознайомитись з інформацією про системи лінійних рівнянь тут