O conceito de sistema e de seus розвязків
Definição: equações Lineares com duas variáveis é uma equação do tipo 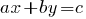 , onde
, onde  e
e  variáveis,
variáveis, 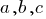 — definidas de um número, para a equação.
— definidas de um número, para a equação.
Solução de equações com duas variáveis é chamado de um par de valores de variáveis, que transforma a equação numa certa igualdade numérica. Este par de valores de variáveis é chamado de solução da equação.
Se dois desconhecidos os valores são vinculados, não uma, mas duas equações, estas equações do sistema linear de equações com duas variáveis.
A solução do sistema de equações com duas variáveis é chamado de um par de números em que cada equação do sistema se transforma em uma verdadeira igualdade numérica.
Um sistema de equações lineares com duas variáveis pode resolver-se de três maneiras:
- Графічнии método de solução de sistemas de equações lineares — em um sistema de coordenadas são construídos os gráficos de duas equações e coordenadas do ponto de intersecção dos gráficos correspondem às raízes de equações. Mais claramente maneira, mas tem a maior margem de erro nos cálculos, pois a precisão da determinação de coordenadas de pontos depende da escala da imagem. Particularmente complexo é a solução de sistemas, quando as taxas ou de raízes de equações fracionárias de um número.
- O método de pesquisa — o mais versátil de todos os métodos de solução de equações lineares com duas variáveis. Ele é usado para praticamente todos os tipos de sistemas de equações. O método de pesquisa é que, a partir de cada equação de um desconhecido se expressa através de um outro desconhecido, e assim até que não obteremos a equação resultante, que será apenas um desconhecido.
- A forma algébrica de adição é muitas vezes usado quando os coeficientes de quando um desconhecido numericamente iguais ou eles podem ser rastreados para a mesma numérico de uma grandeza em рівносильному equação, sem cálculos complexos. A forma algébrica de adição é obter равносильного equação com um dos dados de equações lineares. Adicionando duas equações realizamos a transição para uma equação com uma incógnita.
Solução de sistemas de equações lineares
É uma forma gráfica de soluções de sistemas de equações lineares
Exemplo: Розвяжіть equação: 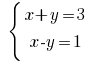
Solução:
Construir gráficos no plano: 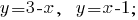
Construindo gráficos de sistemas de equações lineares, podemos ver que os gráficos se cruzam em um ponto E 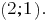
Resposta: 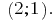
Método de pesquisa para a solução de sistemas de equações lineares
Exemplo: Розвяжіть equação: 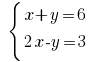
Розв'зування:
A partir da primeira equação expressamos 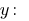
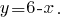
E é obtida a expressão colocamos na segunda equação do sistema:
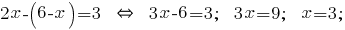
O valor obtido  conectando a expressão
conectando a expressão 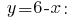
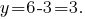
Resposta: 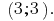
O método de adição para a solução de sistemas de equações lineares
Exemplo: Розвяжіть equação: 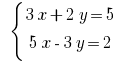
Solução:
Deve livrar-se de uma variável de 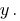 Multiplicar почленно a primeira equação do sistema
Multiplicar почленно a primeira equação do sistema 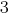 , e a segunda – a
, e a segunda – a 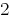 .
.
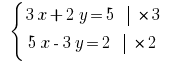
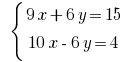
Почленно adicionamos equações lineares e obtemos: 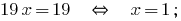
Encontramos o valor  da primeira equação do sistema:
da primeira equação do sistema: 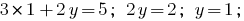
Resposta: 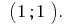
Nota: No método de adição é possível multiplicar não só em números positivos e negativos.
Você também pode visualizar informações sobre o sistema de equações lineares aqui
