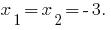Uma equação quadrática, o teorema de Виета

Equações quadráticas

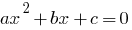Definição: é uma equação Quadrática — equação do tipo , onde 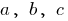— alguns números, e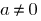

O aspecto geral de uma equação quadrática

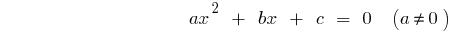
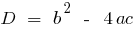— дискриминантов equação quadrática

 

 

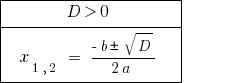
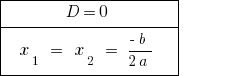
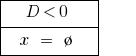
Quando 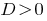— a equação tem dois tipos diferentes de raiz.

Quando — a equação tem duas iguais de raiz. Quando a contagem do número de розвязків é considerado um valor de raiz.

Quando 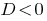— equação de raízes não.

Mestre equação (e = 1)

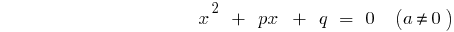
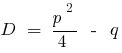— дискриминантов consolidado equação

 

 

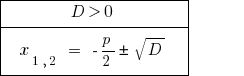
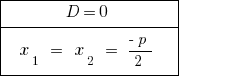
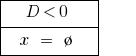
Quando 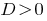— mestre, a equação tem duas formas diferentes de raiz.

Quando — mestre, a equação tem duas iguais de raiz. Quando a contagem do número de розвязків é considerado um valor de raiz.

Quando 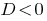— mestre da equação de raízes não.

O teorema Виета em geral,

Se — as raízes de uma equação do segundo grau ,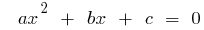

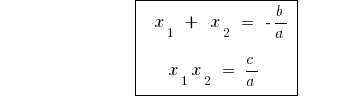
O teorema Виета para resumida, a equação (a=1)

Se — raízes do resumo de uma equação do segundo grau ,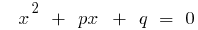

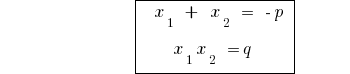
Inversa teorema teorema Виета

Teorema: Se a soma de dois números é igual 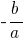, mas uma obra igual 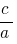, então esses números são raízes da equação quadrática .

 

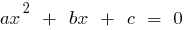Teorema (consolidado equação): Se a soma de dois números é igual 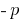, mas uma obra igual 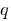, então esses números são raízes da equação quadrática .

 

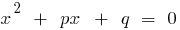A decomposição de um quadrado трехчлена em multiplicadores de

Se — raízes quadrada трехчлена igual a zero 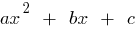(ou seja, as raízes da equaçã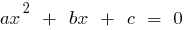o ), o

 

 

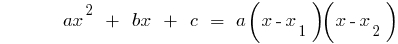
Se дискриминантов quadrado трехчлена é igual a zero (), então 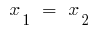, e então

 

 

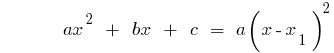
Exemplo. A decomposição трехчлена em multiplicadores de

1. quando
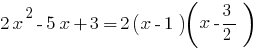
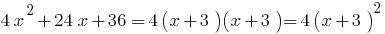
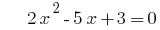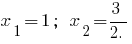
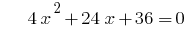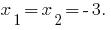
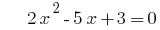2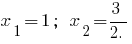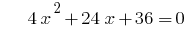. quando