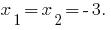Ecuación cuadrática, el teorema de Виета

Ecuaciones cuadráticas

Definición: la ecuación Cuadrática es una ecuación de la especie 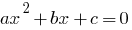, donde 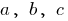— algunos números, y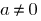

La ecuación general

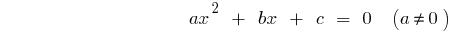
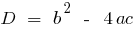— дискриминантов cuadrada de la ecuación

 

 

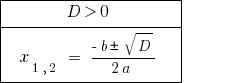
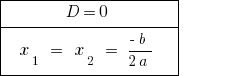
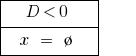
Cuando 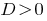— la ecuación tiene dos raíces.

Cuando — la ecuación tiene dos igualdad de raíz. Para calcular la cantidad de розвязків se considera un valor de la raíz.

Cuando 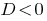— las raíces de la ecuación no.

Resumen de la ecuación (y = 1)

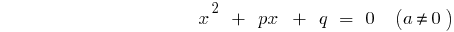
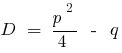— дискриминантов refundido de la ecuación

 

 

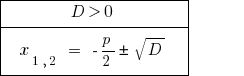
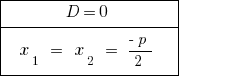
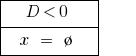
Al 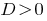— resumen de la ecuación tiene dos raíces.

Al — resumen de la ecuación tiene dos igualdad de raíz. Para calcular la cantidad de розвязків se considera un valor de la raíz.

Al 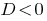— refundida de las raíces de la ecuación no.

El teorema de Виета en el caso general

Si las raíces cuadradas de la ecuación ,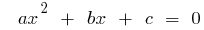

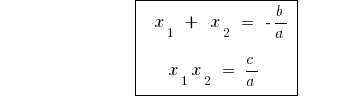
El teorema de Виета para refundido de la ecuación (a=1)

Si las raíces no consolidado cuadrada de la ecuación ,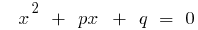

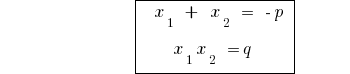
Inversa teorema teorema de Виета

Teorema: Si la suma de dos números es igual 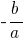, pero la obra es 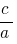, estos números son las raíces cuadradas de la ecuación .

 

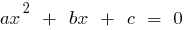Teorema (para refundido de la ecuación): Si la suma de dos números es igual 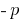, pero la obra es 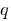, estos números son las raíces cuadradas de la ecuación .

 

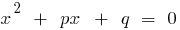La descomposición del cuadrado de la трехчлена en el multiplicador

Si las raíces cuadradas de трехчлена es igual a cero 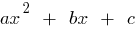(es decir, las raíces de la ecuación ),

 

 

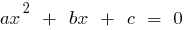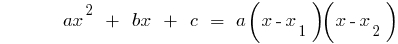
Si дискриминантов cuadrado трехчлена es igual a cero (), 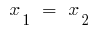y entonces

 

 

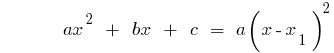
Ejemplo. La descomposición de la трехчлена en el multiplicador

1. cuando
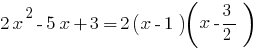
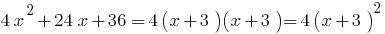
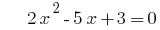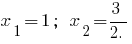
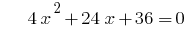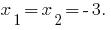
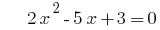2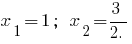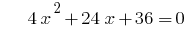. cuando