Definición: Que la función 
está definida en toda la recta numérica. El número 
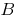se llama en el límite de la función cuando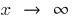 
, si alguno 
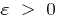se hallare en tal número 
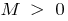, que para todos los 
que cumplan con la condición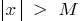 
, se ejecuta la desigualdad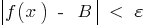 
Si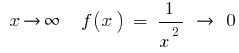 
, es decir, cuando grandes (módulo) de los valores de número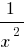 
difiere muy poco de los dígitos 0
Si el comportamiento de la función es diferente cuando 
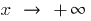y cuando 
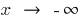, se consideran por separado 
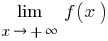(en la definición toman 
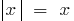) y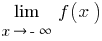 
(en la definición toman 
)
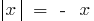El límite de la secuencia de
Ya que la secuencia es una función natural del argumento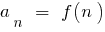 
, la definición de límite de una secuencia cuando 
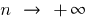concuerda con la definición de límite de una función cuando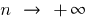
Definición: un Número 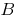se le llama límite de la secuencia 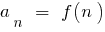, si para cualquier 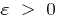existe tal número 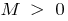, que para todos 
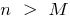, se cumple la desigualdad 
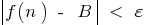es decir,
Si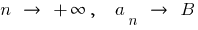 
, lo
Comparar el crecimiento de representación, степенной y logarítmicas funciones
- Cuando
,
es decir,
Si 
, si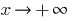 
la función 
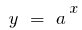crece más rápido que cualquier función 
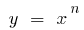, donde 
es un número natural
Gráficamente esta afirmación significa que cuando está lo suficientemente grandes valores de la gráfica de la función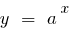 
(donde 
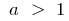) se encuentra por encima de la gráfica de la función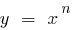 
- Cuando
,
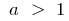
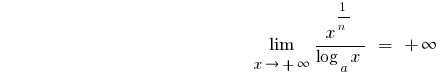es decir,
,
En el caso de grandes ;
,
por lo tanto,
Si , la función 
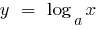crece más lentamente que la función 
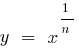(y más lenta que la función 
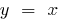o la función 
)
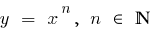Gráficamente esta afirmación significa que cuando está lo suficientemente grandes valores de la gráfica de la función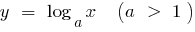 
está por debajo de la gráfica de la función 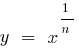(y más aún por debajo de los gráficos de las funciones )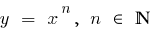