Definição: Deixe a função 
definida em toda a linha do número. O número 
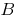é chamado de limite de uma função quando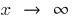 
, se para qualquer 
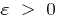achará o número 
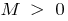que, para todos os 
que satisfazem a condição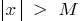 
, é executada a desigualdade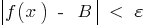 
Quando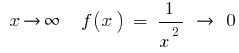 
, isto é, quando o maior (em módulo) os valores de um número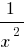 
muito pouco diferente do número de 0
Se o comportamento da função é diferente de quando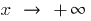 
e quando 
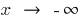, então, separadamente, considerando 
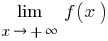(na definição cobram 
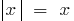) e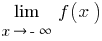 
(na definição cobram 
)
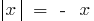Limite de uma seqüência
Como a seqüência é uma função natural do argumento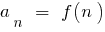 
, então a definição de limite de uma sequência 
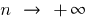, é bastante consistente com a definição de limite de uma função quando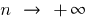
Definição: um Número 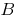é chamado de limite de uma seqüência 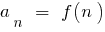, se qualquer 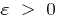, é um número 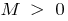que, para todos 
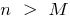, é executada a desigualdade 
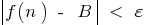т. е.
Se estiver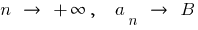 
, então
Comparação de crescimento exponencial, potência e funções logarítmica
- Quando
,
ou seja,
Se 
, quando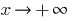 
a função 
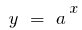cresce mais rápido a partir de qualquer função de potência 
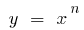, onde a 
é um número natural
Graficamente, esta afirmação significa que se o suficiente para grandes valores de funções de programação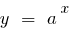 
(onde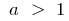 
) está acima do gráfico de uma função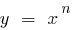 
- Quando
,
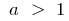
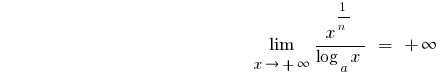ou seja,
,
Quando grandes ;
,
portanto,
Se a , então a função 
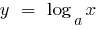cresce mais lentamente que a função 
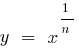(e mais lento, que a função 
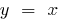ou o recurso 
)
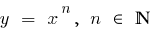Graficamente, esta afirmação significa que se o suficiente para grandes valores de funções de programação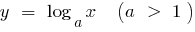 
localizado abaixo do gráfico da função 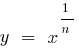(e, ainda mais abaixo dos gráficos de funções )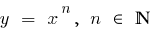