Definição: uma Função  é chamado de periódico com um período de
é chamado de periódico com um período de 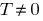 , se para qualquer
, se para qualquer  das áreas de determinar o número
das áreas de determinar o número 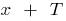 e
e 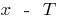 também de entrada na área de definição e
também de entrada na área de definição e
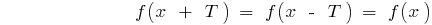 .
.
Propriedades da função periódica
- Se o número -
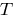 o período de recursos
o período de recursos  , o número
, o número 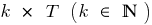 também é o período da função.
também é o período da função. - Se a função é
 periódica de período
periódica de período 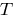 , então a função
, então a função 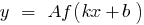 também é periódica e seu período é igual
também é periódica e seu período é igual 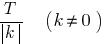
- Se a função é
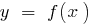 periódica de período
periódica de período 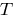 , é compor de uma função (a função da função)
, é compor de uma função (a função da função) 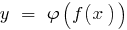 é também periódica com período
é também periódica com período 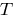 .
. - Para um gráfico de função periódica com período
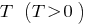 suficiente para construir o gráfico no intervalo de comprimento
suficiente para construir o gráfico no intervalo de comprimento 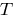 , e depois em paralelo transferir este gráfico ao longo do eixo
, e depois em paralelo transferir este gráfico ao longo do eixo 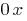 para a distância
para a distância 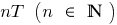 à esquerda e à direita.
à esquerda e à direita.
Exemplos de funções periódicas
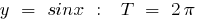
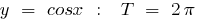
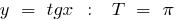
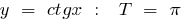

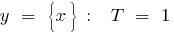
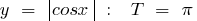
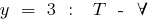

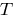 o período de recursos
o período de recursos 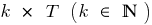 também é o período da função.
também é o período da função. periódica de período
periódica de período 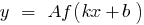 também é periódica e seu período é igual
também é periódica e seu período é igual 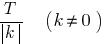
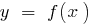 periódica de período
periódica de período 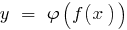 é também periódica com período
é também periódica com período 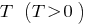 suficiente para construir o gráfico no intervalo de comprimento
suficiente para construir o gráfico no intervalo de comprimento 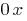 para a distância
para a distância 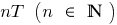 à esquerda e à direita.
à esquerda e à direita.