A continuidade de uma função em um ponto
Definição: uma Função  é chamada de contínua no ponto a
é chamada de contínua no ponto a 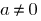 se
se 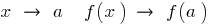 , ou seja,
, ou seja, 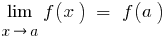 .
.
A continuidade da função no intervalo
Definição: Se a função  é contínua em cada ponto de um período
é contínua em cada ponto de um período  , então é chamada de contínua no intervalo
, então é chamada de contínua no intervalo  .
.
As propriedades de continuidade de uma função
Um exemplo de continuidade de uma função
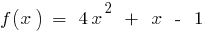 — função contínua (polinômio)
— função contínua (polinômio)
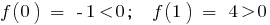 e , portanto, no intervalo (0;1) há um ponto
e , portanto, no intervalo (0;1) há um ponto  em que a função é igual a 0:
em que a função é igual a 0: 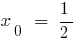
Um exemplo de continuidade de uma função
Um exemplo de continuidade de uma função
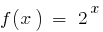 — função contínua. Se
— função contínua. Se
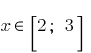 , então
, então 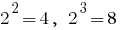 . Porque
. Porque 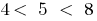 , então, há um ponto
, então, há um ponto  em que
em que 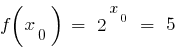 .
.
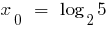
A regra de encontrar a maior e a menor значенб função.
- Se contínua no відрузку
 видуальные adquire nas extremidades desta corte de valores de diferentes caracteres, então em algum ponto desta corte, ela assume um valor igual a zero.
видуальные adquire nas extremidades desta corte de valores de diferentes caracteres, então em algum ponto desta corte, ela assume um valor igual a zero. - Se no intervalo
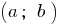 a função
a função  é contínua e não se transforma em zero, o intervalo, a função mantém uma marca permanente.
é contínua e não se transforma em zero, o intervalo, a função mantém uma marca permanente. - A função
 contínua em um intervalo fechado
contínua em um intervalo fechado  , aceita todos os valores intermediários entre os valores desta função em pontos extremos, ou seja, entre
, aceita todos os valores intermediários entre os valores desta função em pontos extremos, ou seja, entre 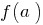 e
e 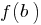 .
. - A função
 contínua em um intervalo fechado
contínua em um intervalo fechado  , limitado neste segmento, ou seja, existem dois números
, limitado neste segmento, ou seja, existem dois números  e
e  que, para todos,
que, para todos, 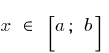 é executada a desigualdade
é executada a desigualdade 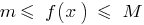 .
. - A soma da diferença e da obra contínua neste intervalo de funções — contínua no mesmo intervalo de função. O quociente de duas funções contínuas — função contínua em todos os pontos em que o denominador não перетвоюється no zero a zero.
- Função inversa à da função contínua em um dado intervalo, é contínua neste intervalo.
- Se a função
 tem derivada no ponto
tem derivada no ponto  , então ela é contínua neste ponto.
, então ela é contínua neste ponto.
Ponto de ruptura
Definição: Ponto a  ponto de estourar a função
ponto de estourar a função 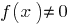 , se o ponto
, se o ponto  não é executada uma condição que, quando
não é executada uma condição que, quando 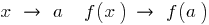 .
.
Exemplos de funções que contenham ponto de ruptura
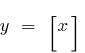 — o ponto de quebra de todos os inteiros de um ponto de
— o ponto de quebra de todos os inteiros de um ponto de
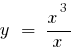 — o ponto de ruptura - 0
— o ponto de ruptura - 0
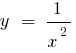 — o ponto de ruptura - 0
— o ponto de ruptura - 0

 видуальные adquire nas extremidades desta corte de valores de diferentes caracteres, então em algum ponto desta corte, ela assume um valor igual a zero.
видуальные adquire nas extremidades desta corte de valores de diferentes caracteres, então em algum ponto desta corte, ela assume um valor igual a zero.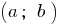 a função
a função 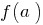 e
e 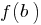 .
. e
e  que, para todos,
que, para todos, 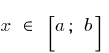 é executada a desigualdade
é executada a desigualdade 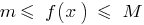 .
.