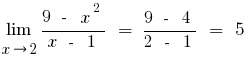
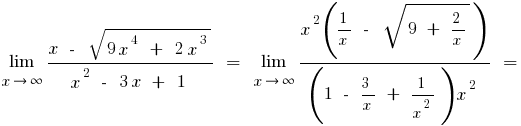
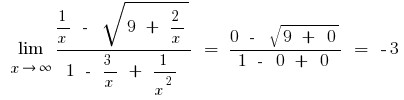
e) tentando decompor o numerador e o pronome em multiplicadores de
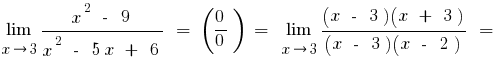
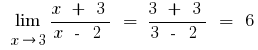
b) se o numerador ou o denominador inclui expressões quadrada ou cúbica da raiz, em seguida, multiplicar o numerador e o denominador na expressão correspondente, para livrar-se as raízes (às vezes introduzem a substituição e a expressão com a raiz indicam uma nova variável)
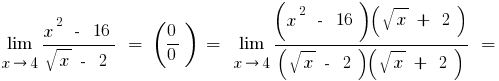
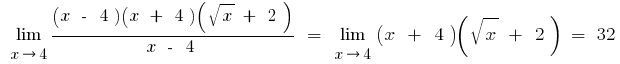
a) se sob o signo do limite custam funções ou funções trigonométricas inversas, tais limites só a primeira de um excelente fronteira

ou suas variações



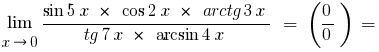
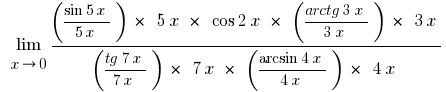
Reduzindo o numerador e o denominador de variáveis, por detrás da parênteses, dado que 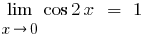 , e dada a перщу excelente fronteira e suas variações, obtemos
, e dada a перщу excelente fronteira e suas variações, obtemos 
- Aproveitando-se da continuidade de funções
 , tentando substituir os valores
, tentando substituir os valores  na função
na função 
- Se calcula o limite, quando
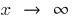 , então tentamos no numerador e местоимении ser levado para fora do parênteses o mais alto grau desconhecido
, então tentamos no numerador e местоимении ser levado para fora do parênteses o mais alto grau desconhecido - Se o resultado da pesquisa
 receberam uma expressão do tipo
receberam uma expressão do tipo 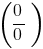 ,
,

 , tentando substituir os valores
, tentando substituir os valores  na função
na função 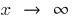 , então tentamos no numerador e местоимении ser levado para fora do parênteses o mais alto grau desconhecido
, então tentamos no numerador e местоимении ser levado para fora do parênteses o mais alto grau desconhecido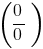 ,
,