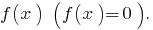Irracional desigualdade

O conceito de irracional desigualdade

Definição: o Irracional desigualdade — desigualdade, contendo a variável sob o signo de raiz -nd.

Solução de equações irracionais

 

O método de intervalos para resolver inequações irracionais

1. Encontrar ОДЗ desigualdade.
2. Encontrar os zeros da função
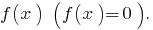
3. Cancelar os zeros da função no ОДЗ e encontrar o sinal da função de cada um dos períodos, em que é dividido ОДЗ .

Exemplo 1:

 

Розвяжіть equação: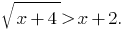

 

Solução: Determinado a desigualdade equivale a desigualdade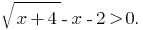

Vamos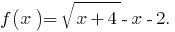

ОДЗ: 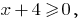, т. е.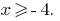

Zeros: 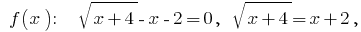tomar no quadrado a esquerda e a direita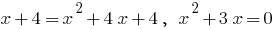

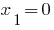- a raiz 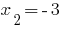- o estranho a raiz.

Resposta: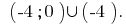

Равносильные de conversão

 

Exemplo 2:

Розвяжіть equação: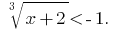

Solução: ОДЗ: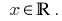

Determinado a desigualdade equivale a неравенствам: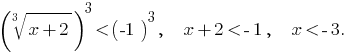

Resposta: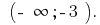

 

 

 

Exemplo 3 :

Розвяжіть equação: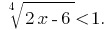

Solução: ОДЗ: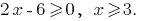

Ambas as partes de um determinado desigualdade невідємні, portanto, ela equivale a неравенствам: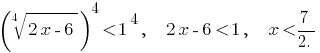

Considerando ОДЗ, recebemos .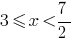

Resposta: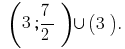

 

 

 

Exemplo 4 :

Розвяжіть equação: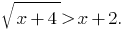

Solução: Determinado a desigualdade equivale a uma população de busca:

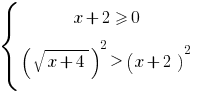ou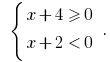

Então 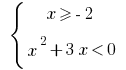ou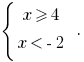

Розвязавши desigualdade 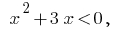temos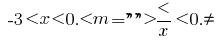

Dada a desigualdade 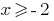, obtemos a solução é o primeiro sistema de

Resposta: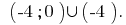

1. Quando поднесении de ambas as partes desigualdade até estranho grau (mantendo o sinal de desigualdade) obtemos a desigualdade, равносильное a esta.
2. Se ambas as partes desigualdade невідємні, durante a elevação de ambas as partes desigualdade a парному grau (mantendo o sinal de desigualdade) obtemos a desigualdade, равносильное a esta.
3. Se ОДЗ especificado desigualdade alguma parte de desigualdade pode adquirir tanto positivos como integrantes de valores e, em seguida, antes de encostar a ambas as partes desigualdade antes парного степеня, nesses casos, vale a pena considerar separadamente.