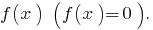Ірраціональні нерівності

Поняття ірраціональної нерівності

Означення: Ірраціональна нерівність — нерівність, що містить змінну під знаком кореня -го степеня.

Розвязування ірраціональних рівнянь

 

Метод інтервалів для розвязування ірраціональних нерівностей

1. Знайти ОДЗ нерівності.
2. Знайти нулі функції
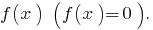
3. Відмінити нулі функції на ОДЗ і знайти знак функції на кожному з проміжків, на які розбивається ОДЗ .

Приклад 1:

 

Розвяжіть рівняння: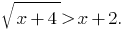

 

Розвязання: Задана нерівність рівносильна нерівності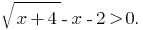

Позначимо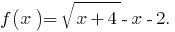

ОДЗ: 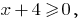, тобто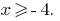

Нулі: 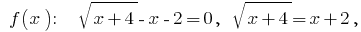підносимо до квадрату ліву і праву частину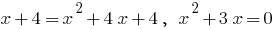

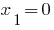- корінь, 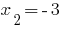- сторонній корінь.

Відповідь: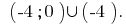

Рівносильні перетворення

 

Приклад 2:

Розвяжіть рівняння: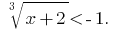

Розвязання: ОДЗ: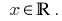

Задана нерівність рівносильна нерівностям: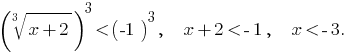

Відповідь: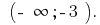

 

 

 

Приклад 3 :

Розвяжіть рівняння: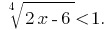

Розвязання: ОДЗ: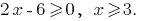

Обидві частини заданої нерівності невідємні, отже, вона рівносильна нерівностям: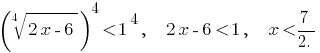

Ураховуючи ОДЗ, одержуємо .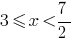

Відповідь: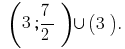

 

 

 

Приклад 4 :

Розвяжіть рівняння: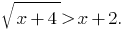

Розвязання: Задана нерівність рівносильна сукупності систем:

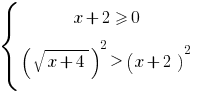або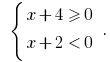

Тоді 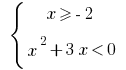або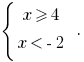

Розвязавши нерівність 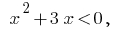маємо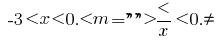

Ураховуючи нерівність 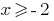, одержуємо розвязок першої системи

Відповідь: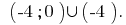

1. При піднесенні обох частин нерівності до непарного степеня (із збереженням знака нерівності) одержуємо нерівність, рівносильну даній.
2. Якщо обидві частини нерівності невідємні, то при піднесенні обох частин нерівності до парного степеня (із збереженням знаком нерівності) одержуємо нерівність, рівносильну даній.
3. Якщо на ОДЗ заданої нерівності якась частина нерівності може набувати як додатних, так і невідємних значень, то, перш ніж підносити обидві частини нерівності до парного степеня, ці випадки слід роглянути окремо.