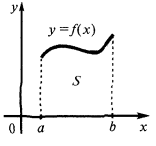
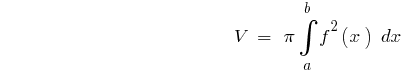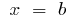Площа криволінійної трапеції
Площа криволінійної трапеції, обмеженої графіком неперервної додатної на відрізку 
функції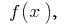 
віссю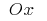 
і прямими 
і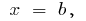 
дорівнює
Приклад.Обчислити площу фігури, обмеженої лініями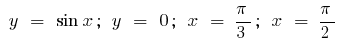 
Зображуючи ці лінії, одержуємо криволінійну трапецію
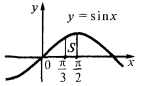
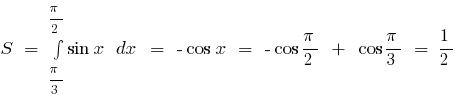
Площа фігури обмеженої графіками двох функцій і прямими 
і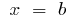 
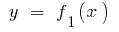Якщо на заданому відрізку неперервні функції 
і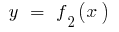 
мають ту властивість, що 
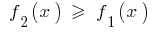для всіх 
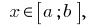то
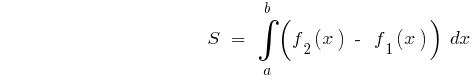
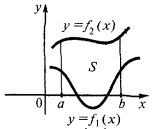
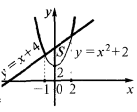
Приклад.Обчислити площу фігури, обмеженої лініями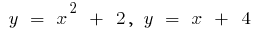 
Зобразимо задані лінії і абсциси їх точок перетину.
Абсциси точок перетину: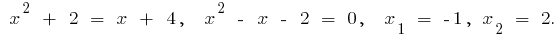 
Тоді за формулою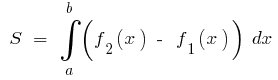 
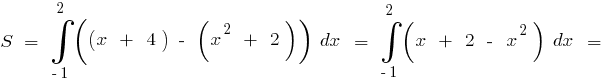
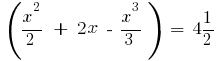
Обєми тіл
У загальному випадку
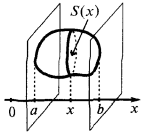
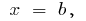Якщо тіло вміщено між двома перпендикулярними до осі площинами, що проходять через точки і то
де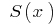 
— площа перерізу тіла площиною, що проходить через точку 
і перпендикулярна до осі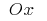
Для тіла обертання
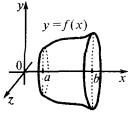
Якщо тіло одержано в результаті обертання навколо осі 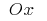криволінійної трапеції, яка обмежена графіком неперервної і невідємної функції 
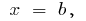на відрізку і прямими і то
