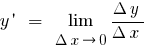
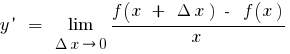
Означення: Похідною функції 
в точці 
називається границя відношення приросту функції в точці до приросту аргументу, коли приріст аргументу прямує до нуля (можна позначити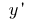 
або 
)
Операція знаходження похідної називається диференціюванням
Поняття приросту аргументу і функції
Приріст аргументу
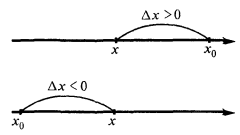
Приріст функції
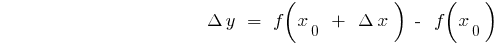
Похідні елементарних функцій
Похідні елементарних функцій знаходяться за допомогою таблиці:
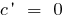
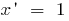
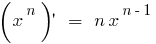
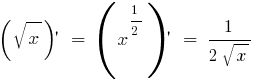
Всі похідні елементарних функцій можна знайти тут!
Складена функція. Як знайти складену функцію
Похідна суми (різниці) двох функцій, кожна з яких має похідну, дорівнює сумі (різниці) похідних цих функцій:
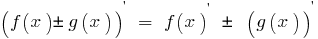
Похідна добутку двох функцій, кожна з яких має похідну, дорівнює сумі добутків кожної функції на похідну другої функції:
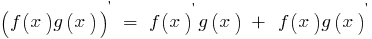
Похідну частки частки двох функцій f(x) і g(x), кожна з яких має похідну і g(x)≠0, знаходять за формулою
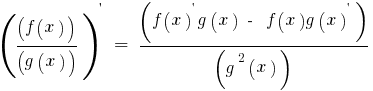
Сталий множник можна виносити за знак похідної:
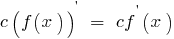
Наведені формули називають правилами диференціювання.
Геометричний зміст похідної
Дотичною до кривої в даній точці 
називається граничне положення січної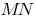 
, коли точка 
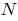наближається вздовж кривої до точки
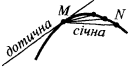
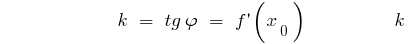— кутовий коефіцієнт дотичної
Рівняння дотичної до графіка функції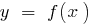 
в точці з абцисою 
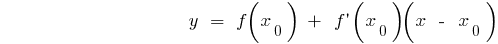
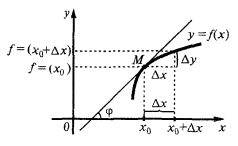
Значення похідної в точці дорівнює кутовому коефіцієнту дотичної до графіка функції в точці з абцисою і дорівнює тангенсу кута нахилу цієї дотичної до осі 
Фізичний зміст похідної
Похідна характеризує швидкість зміни функції при зміні аргументу
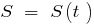— залежність пройденого шляху від часу
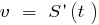— швидкість прямолінійного руху
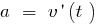— прискорення прямолінійного руху