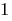Логарифмічні нерівності

Означення: Логарифмічна нерівність — нерівність, в якій змінна знаходиться під знаком логарифма.

Щоб добре вміти розвязувати логарифмічні нерівності, потрібно добре вміти володіти опорними співвідношеннями логарифма.

Рівносильні перетворення найпростіших логарифмічних нерівностей.

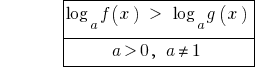
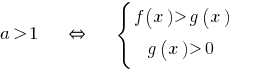
При 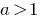знак нерівності не змінюється і враховується ОДЗ.

При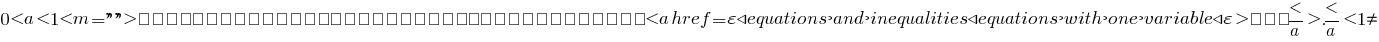

Приклади розвязування найпростіших логарифмічних рівнянь

 

Приклад 1

Розвяжіть рівняння: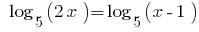

Розвязання:

Оскільки 5>1, то функція 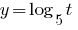— зростаюча і, враховуючи ОДЗ, одержуємо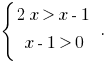

Звідси 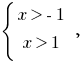тобто

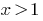
Відповідь: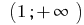

 

Приклад 2

Розвяжіть рівняння: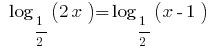

Розвязання:

Оскільки 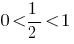, то функція 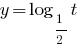— спадна і, враховуючи ОДЗ, одержуємо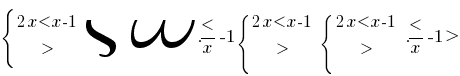

Звідси 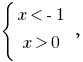— розвязків немає.

Тоді 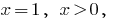тобто

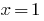
Відповідь: розвязків немає.

Схема розвязування більш складних логарифмічних рівнянь

1. Використання методу інтервалів
2. Використання рівносильних перетворень

Як розвязати логарифмічне рівняння

За допомогою формул логарифмування і потенціювання зводимо рівняння до найпростішого (при цьому враховуємо ОДЗ початкового і стежимо за тим, щоб не втратити корені при звужуванні ОДЗ). Після перетворень, якщо не вдається звести до найпростішого логарифмічного рівняння пробуємо вводити заміну змінних.

Приклади розвязування логарифмічних нерівностей

 

Логарифмічні нерівності розвязуються так само як і логарифмічні рівняння.

Приклад 3 (використання формул логарифмування)

 

Розвяжіть рівняння: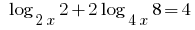

Розвязання:

Перейшовши до основи 2, одержуємо рівносильні рівняння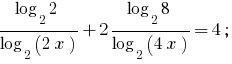

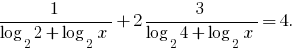
Заміна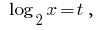

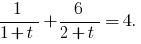
Тоді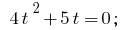

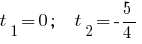
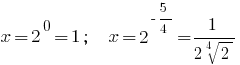
Відповідь: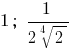

Приклад 4 (використання властивостей логарифмічних функцій)

 

Розвяжіть рівняння: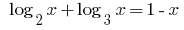

Розвязання:

Функція 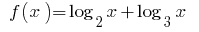зростає на області визначення як сума двох зростаючих функцій, а 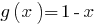спадає. Тому задане рівняння має єдиний корінь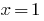

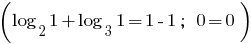
Відповідь: