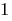Definición: Logarítmica de la desigualdad es la desigualdad, en el que la variable se encuentra bajo el signo de los logaritmos.
Para bien ser capaz de розвязувати logarítmicas de la desigualdad, hay que aprender a manejar los cálculos de los logaritmos.
Tienden a convertir simples logarítmica de las desigualdades.
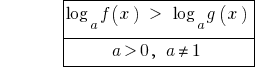
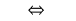
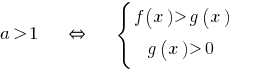
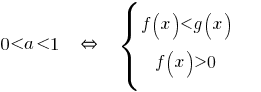
Cuando el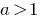 
signo de la desigualdad no cambia y se tiene en cuenta eds.
Cuando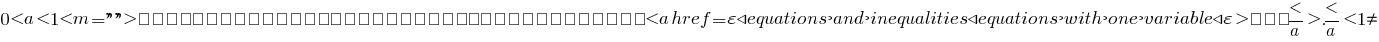 
Ejemplos de decisión simples logarítmica de las ecuaciones de
Ejemplo 1
Розвяжіть de la ecuación: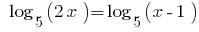 
Soluciones:
Así como 5>1, entonces la función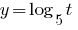 
es creciente y, teniendo en cuenta las eds, obtenemos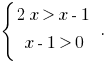 
Desde aquí,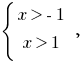 
es decir,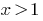 
Respuesta: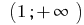 
Ejemplo 2
Розвяжіть de la ecuación: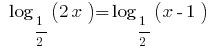 
Soluciones:
Porque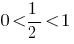 
, entonces la función 
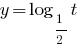es menguante y, teniendo en cuenta las eds, obtenemos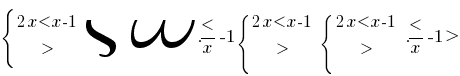 
De aquí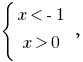 
— розвязків no.
Entonces,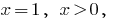 
es decir,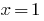 
Respuesta: розвязків no.
El esquema de decisión más complejos logarítmica de las ecuaciones de
Como розвязати logarítmica de la ecuación
Con la ayuda de fórmulas логарифмирования y la potenciacin de la combinamos la ecuación a простейшему (tenemos en cuenta eds inicial y aseguramos de no perder las raíces de la звужуванні eds). Después de la transformación, si no se puede reducir al simple logarítmica de la ecuación intentando introducir la sustitución de variables.
Ejemplos de solución logarítmica de las desigualdades
Logarítmicas de la desigualdad розвязуються así como logarítmicas ecuaciones.
Ejemplo 3 (uso de fórmulas логарифмирования)
Розвяжіть de la ecuación: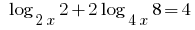 
Soluciones:
Yendo a la base 2, obtenemos constituían la ecuación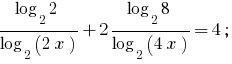 
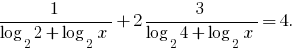
Sustitución de la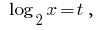 
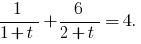
Entonces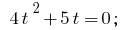 
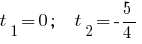
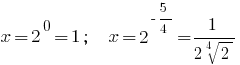
Respuesta: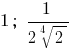 
Ejemplo 4 (uso de las propiedades de las funciones logarítmica)
Розвяжіть de la ecuación: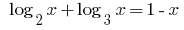 
Soluciones:
La función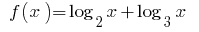 
crece en el ámbito de la definición 
como la suma de dos funciones crecientes y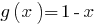 
viene. Por lo tanto, especificado por la ecuación tiene una única raíz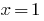
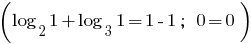
Respuesta: 