Definición: la Asíntota de la curva es una recta a la que se aproxima indefinidamente la curva cuando se elimina ii en нескінечність.
Las asíntotas verticales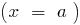 
— vertical asíntota, 
cuando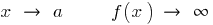 
Vertical asíntota puede ser en un punto 
, si el punto limita abiertos de los intervalos de la definición de esta función y el punto de la función tiende a infinito.
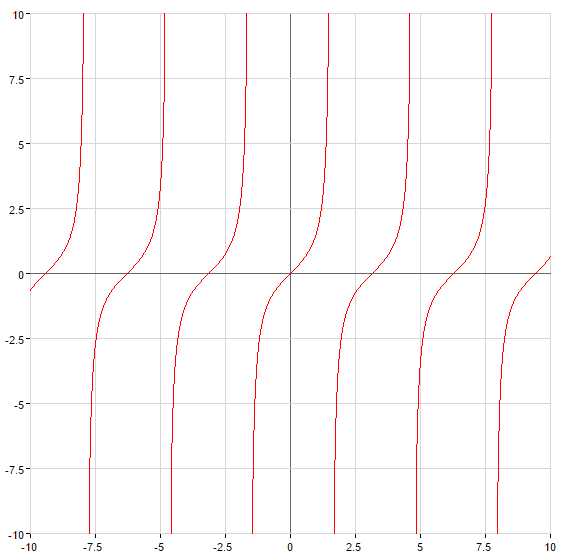
Ejemplos de asíntotas verticales
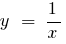
Cuando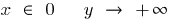 
Cuando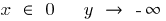 
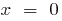— asíntota vertical
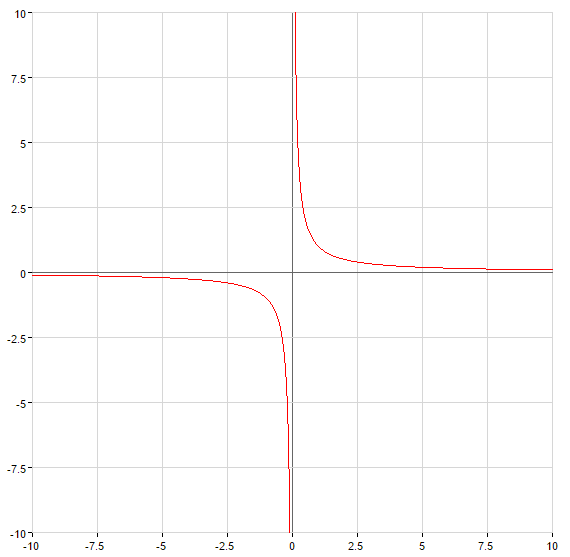
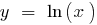
Cuando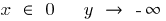
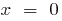— asíntota vertical
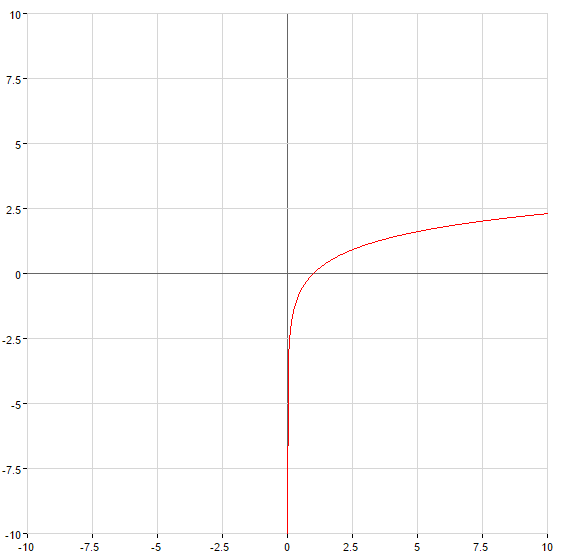
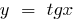
Cuando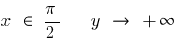 
Cuando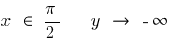 
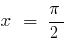— asíntota vertical
Inclinados y horizontales asíntotas 
- Si
— drobno-función racional en la que el grado del numerador en una unidad mayor que el grado del denominador, distinguiendo la parte entera y utilizamos la definición de las asíntotas. - En el caso general de la ecuación de los planos inclinados y horizontales asíntotas pueden obtenerse con el uso de fórmulas
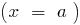
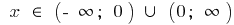
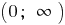
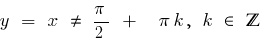
— drobno-función racional en la que el grado del numerador en una unidad mayor que el grado del denominador, distinguiendo la parte entera y utilizamos la definición de las asíntotas.