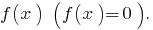El concepto de lo irracional de la desigualdad
Definición: Irracional de la desigualdad 
es la desigualdad, que contiene la variable bajo el signo de la raíz -segundo grado.
Solución de ecuaciones exponenciales
El método de los intervalos para la solución de inecuaciones irracionales
- Encontrar las eds de la desigualdad.
- Encontrar los ceros de la función
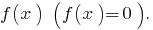
- Cancelar los ceros de la función de la eds y encontrar el signo de la función en cada uno de los períodos en que se divide la eds .
Ejemplo 1:
Розвяжіть de la ecuación: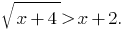 
Solución: valor Nominal de la desigualdad es equivalente a la desigualdad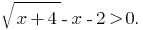 
Designaremos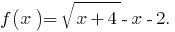 
Eds: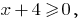 
, es decir,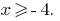 
Ceros: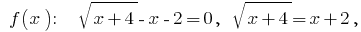 
ofrecemos en el cuadrado de la izquierda y la derecha la parte de la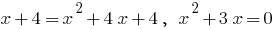 
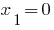- la raíz 
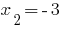- manchas de la raíz.
Respuesta: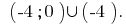
Tienden a convertir
Ejemplo 2:
Розвяжіть de la ecuación: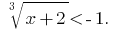 
Solución: eds: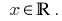 
Valor nominal de la desigualdad equivale a неравенствам: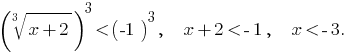 
Respuesta: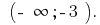
Ejemplo 3 :
Розвяжіть de la ecuación: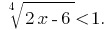 
Solución: eds: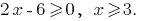 
Ambos lados de la parte especificada de la desigualdad невідємні, por lo tanto, es equivalente a la неравенствам: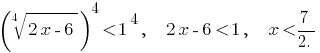 
Teniendo en cuenta la salud, en la que recibimos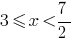 
.
Respuesta: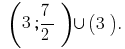
Ejemplo 4 :
Розвяжіть de la ecuación: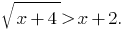
Solución: valor Nominal de la desigualdad equivale a la población de sistemas:
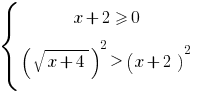o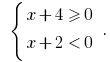 
Entonces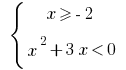 
o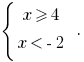 
Розвязавши la desigualdad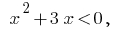 
tenemos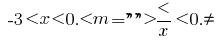 
Teniendo en cuenta la desigualdad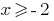 
, obtenemos la solución de la primera de un sistema de 
Respuesta: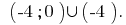
- Al ofrecer ambas partes de la desigualdad hasta el grado impar (manteniendo el signo de la desigualdad), se obtiene la desigualdad que constituyen este.
- Si ambas partes de la desigualdad невідємні, al elevar ambos lados de la desigualdad a парному grado (manteniendo el signo de la desigualdad), se obtiene la desigualdad que constituyen este.
- Si en las eds teórico de la desigualdad, una parte de la desigualdad se puede adquirir tanto positivos como integrante de valores, antes de dar a ambos lados de la parte de la desigualdad a la asociación степеня estos casos vale la pena considerar por separado.