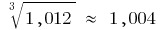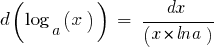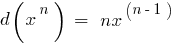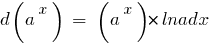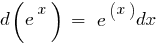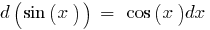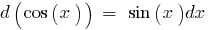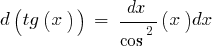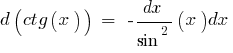El concepto de diferencial
Definición: el Diferencial de la función 
en el punto 
se llama la obra derivada 
en ese punto, es decir, 
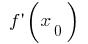en el crecimiento del argumento 
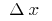(denotado por 
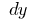o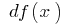 
— se lee "te игрек")
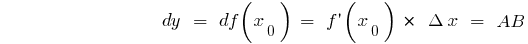
Para cualquier punto 
: 
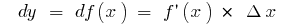si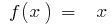 
, tenemos 
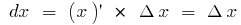, entonces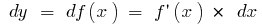 
La tabla de los diferenciales elementales funciones:
Ejemplo hallar el diferencial en las matemáticas:
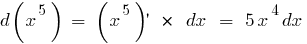
El diferencial derivada de la función
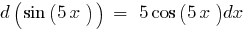
La principal propiedad del diferencial
El diferencial de la función principal lineal (es decir, proporcional a la 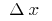parte del incremento de la función
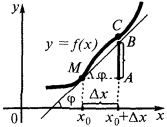
Encontrar el diferencial. Geométrico significado de la diferencial.
Las reglas de la posición diferencial son los mismos que para hallar la derivada, sólo es necesario multiplicar la derivada en dх.
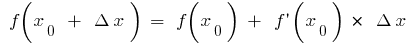
Si en la fórmula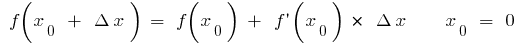 
(cuando la ha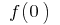y 
, y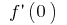 
), entonces para los pequeños 
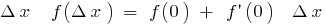. Se denota 
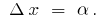Entonces para los pequeños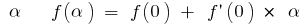 
Por ejemplo:
a)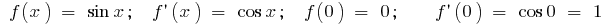 
, es decir 
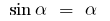(para los pequeños 
) ;
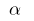b)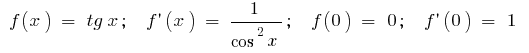 
, es decir 
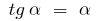(para los pequeños )
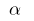Ejemplo del cálculo diferencial Para gafas de cálculo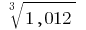 
tomaremos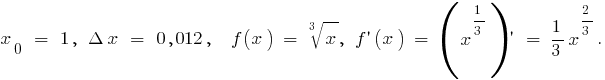 
Entonces,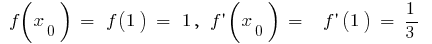 
la fórmula 
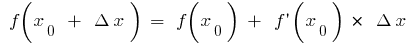da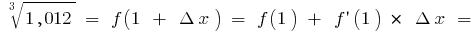 
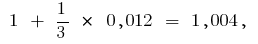es decir, 