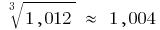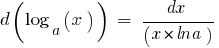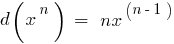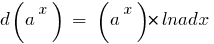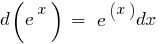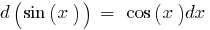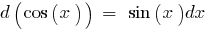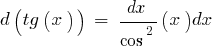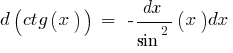The concept of differential
Definition: the Differential of the function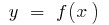 
at point 
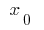is defined as a product of the derivative 
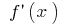at this point, that is, 
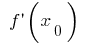the increase of the argument 
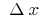(denoted by 
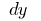or 
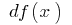— read "teh y")
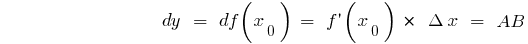
For any point 
: 
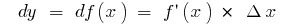if you 
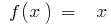have 
, then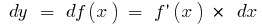 
Table of differentials of elementary functions:
An example of finding a differential in mathematics:
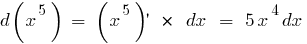
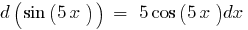
The main property of differential
Differential of a function-the main linear (i.e. proportional 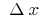) part of the increment function
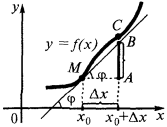
The finding of the differential. The geometrical meaning of the differential.
The rules for finding the differential remains the same as that for finding the derivative, you only need to multiply the derivative on DX.
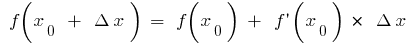
If in formula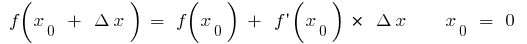 
(when there are 
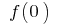and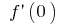 
), then for small 
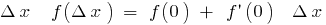. Let us denote 
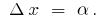Then for small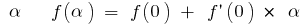 
For example:
a)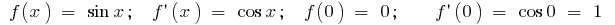 
, that is 
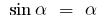(for small 
) ;
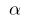b)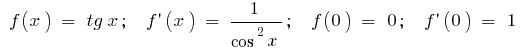 
, that is 
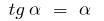(for small )
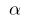An example of calculating the differentials For numerical calculations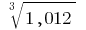 
we take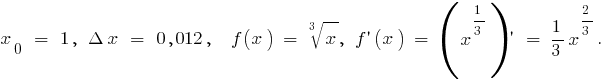 
Then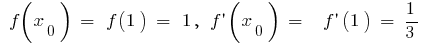 
the formula 
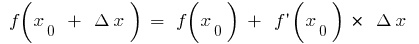gives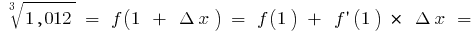 
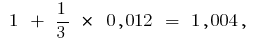that is 