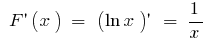Original
Definition: a Function 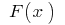 is called the initial function
is called the initial function 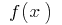 on this interval, if any
on this interval, if any 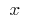 of this period
of this period 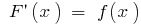
Examples
- For functions
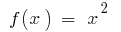 on the interval
on the interval 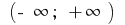 initial is
initial is 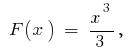 because
because 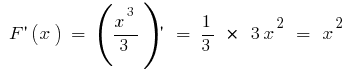
- For functions
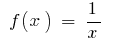 on the interval
on the interval 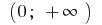 initial is
initial is 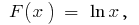 because
because 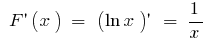
The main property of the integral
If the function 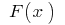 is the initial function
is the initial function 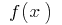 on this interval and
on this interval and 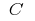 is an arbitrary constant, the function
is an arbitrary constant, the function 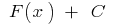 is also the initial function
is also the initial function 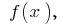 in this case, any primitive of the function
in this case, any primitive of the function 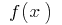 on this interval can be written in the form
on this interval can be written in the form 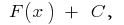 where
where 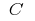 is an arbitrary became
is an arbitrary became
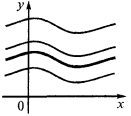
The geometric meaning
Any graphics primitive of this function can be obtained from each other by parallel transfer along the axis 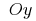
Indefinite integral
Definition:the Set of all primitives of a given function 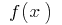 is called the indefinite integral and is denoted by
is called the indefinite integral and is denoted by 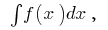 i.e.,
i.e., 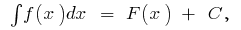 where
where 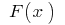 one of the primitive functions
one of the primitive functions 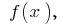 and
and 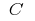 some became
some became
Rules of integration
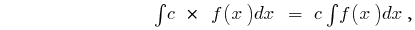 where
where 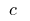 became
became
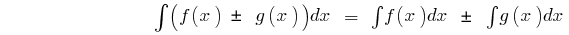
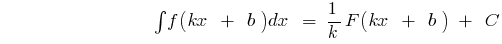

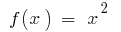 on the interval
on the interval 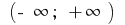 initial is
initial is 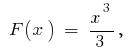 because
because 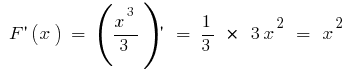
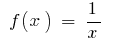 on the interval
on the interval 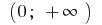 initial is
initial is 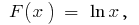 because
because