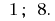The concept of the irrational equation
Definition: an Irrational equation 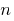 is an equation containing the variable under the root sign
is an equation containing the variable under the root sign 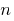 of the first degree.
of the first degree.
Solution of irrational equations
- With the rise of both parts of the equation are irrational to one extent
- Using the change of variables
In the presentation of both parts of the equation to the degree is odd (1,3,5,7....) the resulting equation is equivalent to a given ( DHS)
Example 1:
Rozwarte equation: 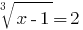
Solutions: 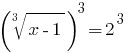
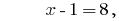
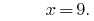
Answer: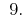
In the presentation of both sides of the pair degree in (2,4,6,8....) can appear extraneous roots, which will eliminate checking.
Example 2:
Rozwarte equation: 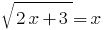
Solutions: 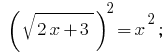
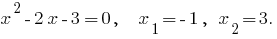
Check: When you 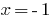 have
have 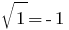 is not a correct equation, therefore,
is not a correct equation, therefore, 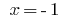 is an extraneous root.
is an extraneous root.
If you 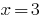 have
have 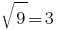 - a true equality, therefore,
- a true equality, therefore, 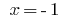 is the root of the given equation.
is the root of the given equation.
Answer: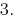
If in the equation variable occurs in the same form, suchno the corresponding expression with a variable to mark one letter (a new variable).
Example 3:
Rozwarte equation: 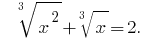
Solution: Let Us Denote 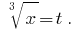 Then
Then 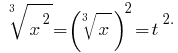
We obtain the equation: 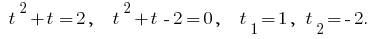
Reverse the substitution: 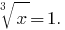 Then
Then 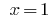 or
or 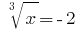 here
here 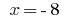 .
.
If you 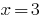 have
have 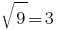 - a true equality, therefore,
- a true equality, therefore, 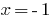 is the root of the given equation.
is the root of the given equation.
Answer: