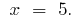Diagram solving equations, change of variables

Solving equations using equations and effect

1. Conversion, guaranteeing the preservation of the right of equality
2. Checking the roots by substitution into the original equation

Solving equations by using equivalent transformations

1. Note IDS equal for both forward and reverse transformations
2. Save on DHS equal for both forward and reverse transformations

The solution of equations. The change of variables

If in the equation variable occurs in the same form, whether the corresponding expression with a variable to mark one letter (a new variable).

Example 1.

Rozwarte equation: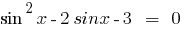

Rozwiazania.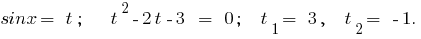

1. If 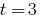the equation 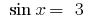has no roots because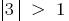

2. If you 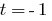have 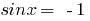, then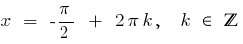

Answer: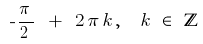

Example 2.

Rozwarte equation: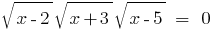

Rozwiazania. Because under the root sign pair forms can stand alone newmn expression, then the region of acceptable values (IDS) of the given equation is given by a system 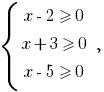rozvyazka which is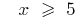

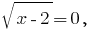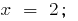
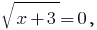The product is equal to zero if and only if one of the multipliers equal to zero, and all other multipliers exist: when 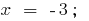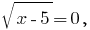when when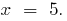

The value 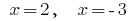is not included in the odz of the given equation, therefore, they are not the roots of the given equation.

The value 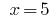included in the DHS, so 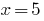is a root of the given equation.

Answer: