Definition: a Geometric progression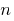 
is a numerical sequence, the first member of which is nonzero, and each member, starting with the second, equal to the previous member, multiplied by the same number not equal to zero.
Definition: the Denominator of a geometric progression 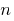is constant for the sequence number 
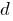, which is multiplied by each member.
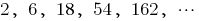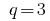
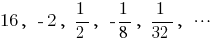— geometric progression,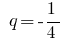 
— geometric progression, 
— geometric progression
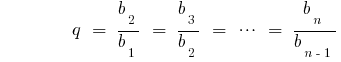— the denominator of a geometric progression
The characteristic properties of geometrical progression
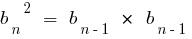
Property: the Square of any member of a geometric progression (starting from the second term) equal to the product of the previous and the next members, and Vice versa, if you vlastiti specified, the sequence is a geometric progression.
Formula of nth member of geometric progression
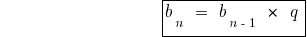
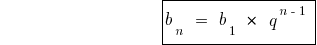
Formula sum of first n members of a geometric progression
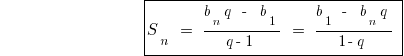
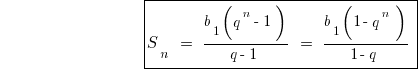
Plan solve problems on geometric progression
- Everything that is said in the speech tasks (members progress their amount, etc.) expressed through the first term and the difference of progression.
- Make the equation (or system of equations) according to the problem. In the case when the task of the transition from a geometric progression to an arithmetic progression and Vice versa, to form equations of the normally used characteristic properties of progressions.
Infinitely decreasing geometric progression
Definition: an Infinitely decreasing geometric progression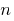 is an infinite geometric progression, and the denominator of which modulus less than unity 
.
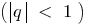Example
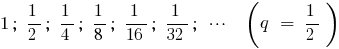
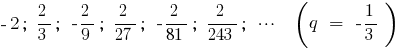
Definition: the Sum of infinitely decreasing geometric progression is a limit, towards which the sum of 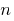its first members, at infinite growth .
.
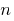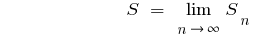
The formula to calculate the sum of an infinitely decreasing geometric progression
Example of finding the sum of an infinitely decreasing geometric progression
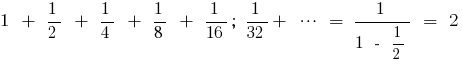
Converting a recurring decimal in the usual
Example
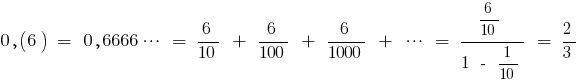(as the sum of infinitely decreasing geometric progression with the first member 
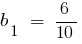and the denominator 
)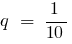