The monotony and continuity of functions
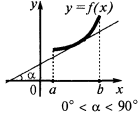
A sufficient condition for increasing functions
If at each point of the interval 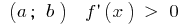 , the function is increasing on this interval
, the function is increasing on this interval
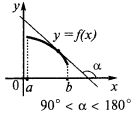
A sufficient condition for decreasing functions
If at each point of the interval 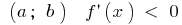 , the function is decreasing on this interval
, the function is decreasing on this interval
Remark. These conditions are only sufficient but not necessary conditions for growth and decreasing functions
A necessary and sufficient condition of constancy of the function
A function 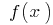 is constant on an interval
is constant on an interval 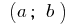 if and only if when
if and only if when 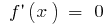 all points of the interval
all points of the interval
The extrema (maximums and minimums) of the function
The maximum point
Definition: the Point 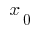 of defining functions
of defining functions 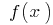 is called a maximum point of this function if there
is called a maximum point of this function if there 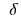 is a neighborhood
is a neighborhood 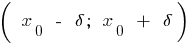 of the point
of the point 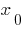 that for all
that for all 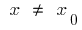 from this neighborhood inequality
from this neighborhood inequality 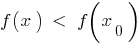
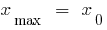 — the maximum point
— the maximum point
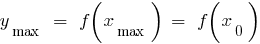 — max
— max
The point of a minimum
Definition: the Point 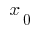 of defining functions
of defining functions 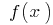 is called the minimum point of this function if there
is called the minimum point of this function if there 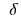 is a neighborhood
is a neighborhood 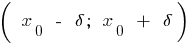 of the point
of the point 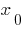 that for all
that for all 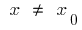 from this neighborhood inequality
from this neighborhood inequality 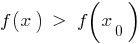
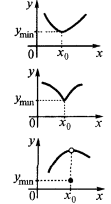
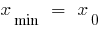 — minimum point
— minimum point
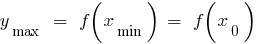 — minimum
— minimum
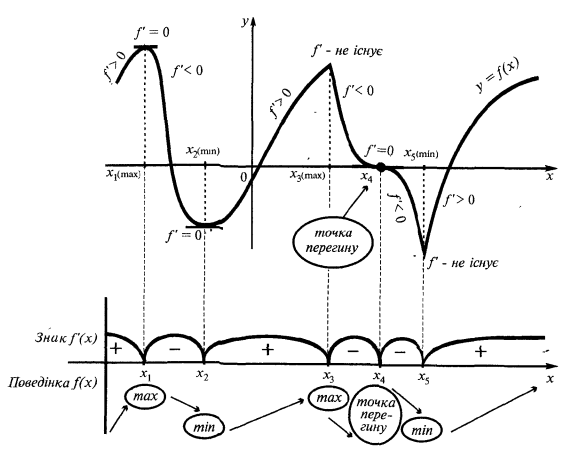
The critical point
Definition: the Interior points of the domain of definition of functions where the derivative is zero or does not exist are called critical
Necessary condition for an extremum
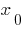 — the extremum point
— the extremum point 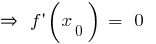 or
or 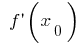 not exists
not exists
(but not at each point 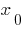 where
where 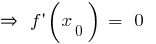 or
or 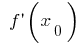 not there will be an extremum!)
not there will be an extremum!)
Sufficient condition of extremum
at the point of 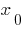 sign
sign 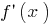 changes
changes 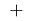 at
at 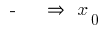 point of maximum
point of maximum
at the point the 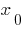 sign
sign 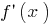 changes
changes 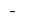 at the
at the 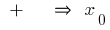 point of minimum
point of minimum
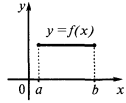
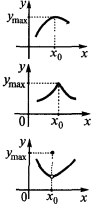
An example of a graph of a function 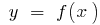 that has an extremum
that has an extremum
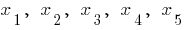 — critical point
— critical point
The study of the function on the monotonicity and extrema
- Find the domain of definition and the intervals on which the function is continuous
- To find the derivative
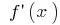
- Find the critical points, i.e. the interior points determining where
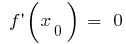 or not there
or not there - Denote the critical point on the domain of definition, find sign of derivative and nature of function at each interval, which splits the definition area
- For each critical point determine whether it is high or low or is not an extremum point
- Record porni the result of the study (intervals of monotonicity and extrema)
Example. 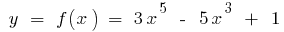
Scope: 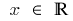
The function is continuous at every point of its domain of definition
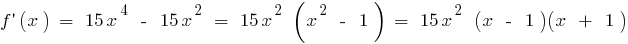
 there is in the entire scope
there is in the entire scope
 when
when 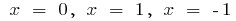
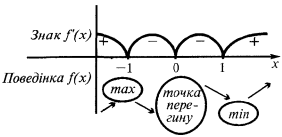
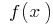 increases with
increases with 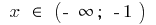 and
and 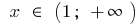
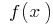 subsides when
subsides when 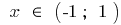
Extreme points: 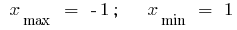
Extremes: 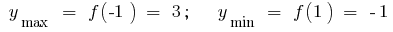
Maximum and minimum values of continuous functions on the interval
Property: If the function is 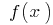 continuous on an interval and has therein a finite number of critical points, then it attains its maximum and minimum values on this interval either at a critical point belonging to this interval or at the endpoints of the interval
continuous on an interval and has therein a finite number of critical points, then it attains its maximum and minimum values on this interval either at a critical point belonging to this interval or at the endpoints of the interval
Finding maximum and minimum values of continuous functions on the interval
- To find the derivative
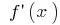
- Find the critical points (
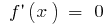 or not exists)
or not exists) - Choose critical points that belong to a given segment
- To calculate the function values at critical points and the endpoints of the interval
- Compare the two values and choose the smallest and largest
Example. 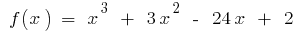 when
when 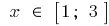
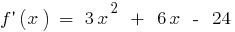
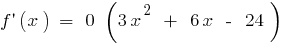 if
if 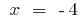 and when
and when 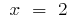
A given segment 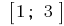 belongs to only critical point
belongs to only critical point 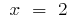
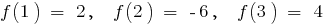


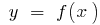 that has an extremum
that has an extremum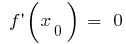 or not there
or not there