Definition: Let be a function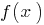 
defined on the entire number line. The number 
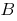is called the limit of the function 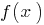at 
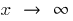if for any 
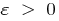there exists a number 
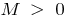that for all 
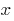satisfying the condition 
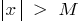, the following inequality is satisfied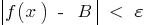 
If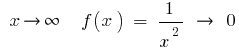 
, that is, for large (absolute) values of the number 
very little different from the number 0
If the behavior 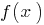is different with 
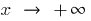and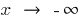 
separately consider 
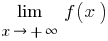(in the definition of take 
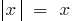) and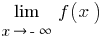 
(definition of take 
)
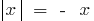The limit of a sequence
Since a sequence is a function of natural argument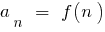 
, the definition of limit of a sequence with 
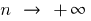is identical to the definition of limit of a function at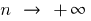
Definition: a Number 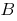is called the limit of a sequence 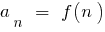if for any 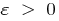there is such number 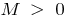that for all 
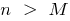, the following inequality is satisfied 
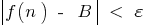i.e.
If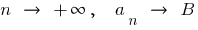 
,
Comparison of exponential growth, exponential and logarithmic functions
,
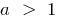
that is
If 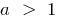, when 
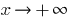a function 
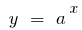grows faster than any exponential function 
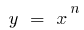where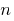 
is a natural number
Graphically, this statement means that for sufficiently large values of 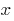the graph of the function 
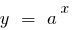(where 
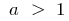) is above the graph of a function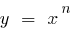 
,
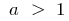
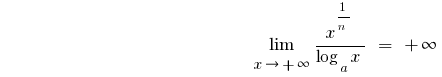that is
,
At large ;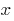
,
so
If 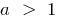, the function 
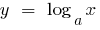increases slower than the function 
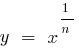(and especially slower than a function 
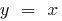or a function 
)
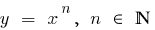Graphically, this statement means that for sufficiently large values of 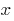the graph of the function 
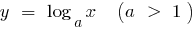lies below the graph of a function 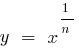(and especially below the graphs of functions )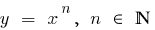