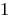Definition: Logarithmic equation — an equation in which the variable is under the sign of logarithm..
So good to be able rozwiazywanie logarithmic equations, you need to be able to control the reference ratio of the logarithm.
Equivalent transformation of simple logarithmic equations.
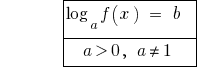
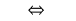
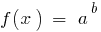
Since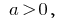 
the 
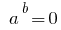DHS and therefore the initial equation is automatically taken into account.
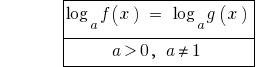
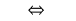
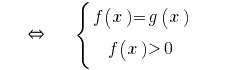or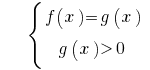 
Examples of the solution of the simplest logarithmic equations
Example 1
Rozwarte equation: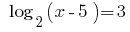 
Solutions:
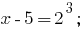
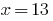
Answer: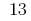 
Example 2
Rozwarte equation: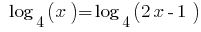 
Solutions:
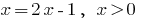(DHS also considered)
Then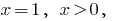 
that is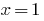 
Answer: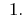 
The scheme is more complex logarithmic equations
- The use of equations and effect
- Using the properties of the relevant functions
- The use of equivalent transformations
As razvesti logarithmic equation
Using the formulae of logarithm and potentiating reduce the equation to a simple (consider the initial DHS and make sure not to lose roots when sujuan DHS). After transformation, if it is not possible to reduce to a simple logarithmic equations we are trying to introduce a change of variables.
Examples of the solution of logarithmic equations
Example 3 (use of formulas, logarithms)
Rozwarte equation: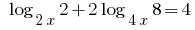 
Solutions:
Going to the base 2, we get the equivalent equation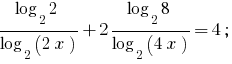 
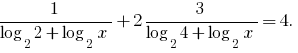
Replacement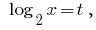 
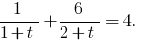
Then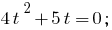 
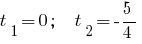
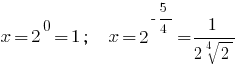
Answer: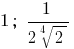 
Example 4 (using properties of logarithmic functions)
Rozwarte equation: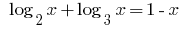 
Solutions:
The function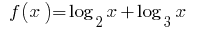 
increases in scope 
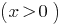as the sum of two increasing functions, and 
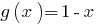comes. Therefore, the given equation has a single root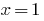
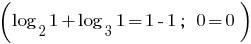
Answer: 