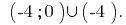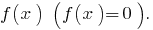The concept of the irrational inequality
Definition: Irrational inequality  an inequality that contains a variable under the sign of root
an inequality that contains a variable under the sign of root  -degree.
-degree.
Solution of irrational equations
Interval methods for the solution of irrational inequalities
- Find DHS inequality.
- Find the zeros of the function
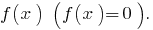
- To cancel the zeros of the function at DHS and find the sign function on each of the intervals which split the DHS .
Example 1:
Rozwarte equation: 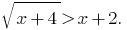
Solution: the Given inequality is equivalent to inequality 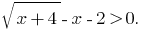
We denote 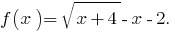
DHS: 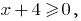 i.e.
i.e. 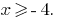
Zeros: 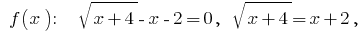 put into the square left and right side
put into the square left and right side 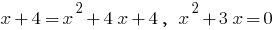
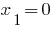 - the root
- the root 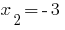 is outside the root.
is outside the root.
Answer: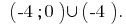
Equivalent conversion
- In the presentation of both parts of the inequality to an odd degree (with preservation of the inequality sign) we get the inequality, tantamount given.
- If both sides of an inequality newmn, when you lift both parts of the inequality to the pair of degrees (preserving the sign of the inequality) we get the inequality, tantamount given.
- If DHS inequality given some part of the inequality can acquire both positive and integral values, before bringing both parts of the inequality to the pair anymore, these cases should be considered separately.
Example 2:
Rozwarte equation: 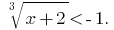
Solution: DHS: 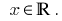
The given inequality is equivalent to the inequalities: 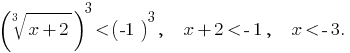
Answer: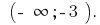
Example 3 :
Rozwarte equation: 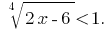
Solution: DHS: 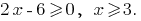
Both parts of the given inequality newmn, therefore, it is equivalent to the inequalities: 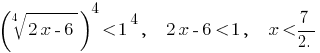
Given DHS obtained 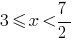 .
.
Answer: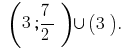
Example 4 :
Rozwarte equation: 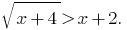
Solution: the Given inequality is equivalent to the set of systems:
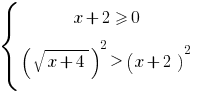 or
or 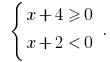
Then 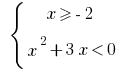 or
or 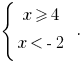
Rozwadowski inequality 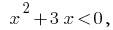 have
have 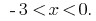
Given the inequalities 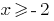 , we obtain the solution of the first system
, we obtain the solution of the first system 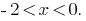 . The solution of the second system:
. The solution of the second system: 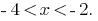 Obanyaki of these solutions, we get the answer.
Obanyaki of these solutions, we get the answer.
Answer: