The concept of the second derivative



Suppose the function 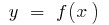 has a derivative
has a derivative 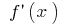 at all points of some interval. This derivative, in turn, is a function of
at all points of some interval. This derivative, in turn, is a function of 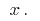 If the function
If the function 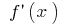 is differentiated, its derivative is called the second derivative
is differentiated, its derivative is called the second derivative 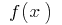 and denoted
and denoted 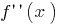 (or
(or 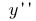 )
)
Example. 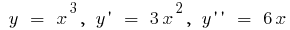
The concept of convexity, concavity and points of inflection of the graph funct
Let the function 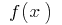 defined on the interval
defined on the interval 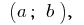 and at the point
and at the point 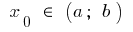 has a finite derivative. Then schedule this function at the point
has a finite derivative. Then schedule this function at the point 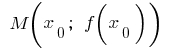 can hold tangent
can hold tangent
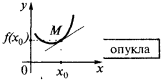
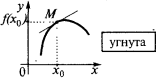
If in some neighborhood of the point  all the points of the curve graph of a function
all the points of the curve graph of a function 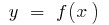 (except for the points
(except for the points 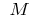 ) lie above the tangent line, then we say that the curve (function) at the point
) lie above the tangent line, then we say that the curve (function) at the point  is convex (more precisely, strictly convex). Also it is sometimes said that in this case the function graph
is convex (more precisely, strictly convex). Also it is sometimes said that in this case the function graph 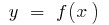 is convex down
is convex down
If in some neighborhood of the point  all the points of the curve (except the points
all the points of the curve (except the points 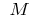 ) lie below the tangent, then we say that the curve (function) at the point
) lie below the tangent, then we say that the curve (function) at the point  is potou (or rather, strictly potou). Also it is sometimes said that in this case the function graph is convex up
is potou (or rather, strictly potou). Also it is sometimes said that in this case the function graph is convex up
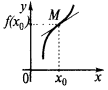
If the point is 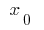 on the x-axis has the property that if the argument
on the x-axis has the property that if the argument 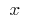 through the curve
through the curve 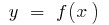 passes from one side to the other tangent, then the point
passes from one side to the other tangent, then the point 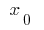 is called the inflection point of the function
is called the inflection point of the function 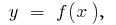 point curve
point curve 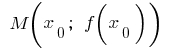 — point of inflection of the graph of a function
— point of inflection of the graph of a function 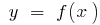
 the point of inflection of the graph of a function
the point of inflection of the graph of a function
 the inflection point of the function
the inflection point of the function
In some neighborhood of the point 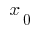 : when
: when 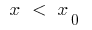 the curve is below the tangent, and when
the curve is below the tangent, and when 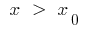 the curve is above the tangent (or Vice versa)
the curve is above the tangent (or Vice versa)
The study of the function of the bulge, unott and inflection points
Example. 
- To find the scope and the intervals on which the function is continuous
- Find the second derivative
- Find an internal point of determining where
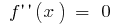 or not there
or not there - Mark the resulting point on the scope, find the sign of the second derivative and the behavior of the function on each interval, which splits the definition area
- To record the desired outcome of the study (intervals of convexity and concavity and points of inflection)
Scope: 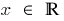
The function is continuous at every point of its domain of definition
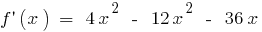
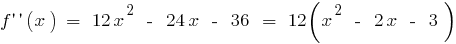
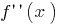 there is in the entire scope
there is in the entire scope
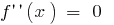 when
when 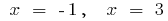
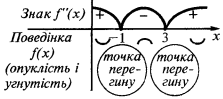
In the interval 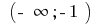 and in the interval
and in the interval 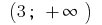 graph of a function
graph of a function 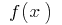 convexity directed downwards
convexity directed downwards 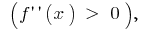 and in the interval
and in the interval  the graph of the function
the graph of the function 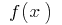 sent bump up
sent bump up 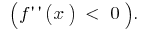
Inflection points: 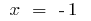 i
i 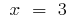 (at these points
(at these points 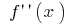 changes the sign)
changes the sign)

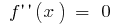 or not there
or not there