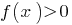Equivalent transformation of simple inequalities
 When a > 1
When a > 1
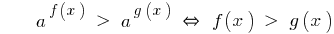
The inequality sign is preserved.
Example 1
Rozwarte inequality: 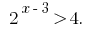
Solutions:
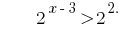
A function 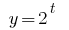 is increasing, therefore equate indices,
is increasing, therefore equate indices,
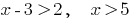
Answer: 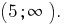
 If 0 < a < 1
If 0 < a < 1
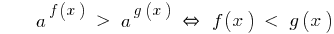
The inequality sign is reversed.
Example 2
Rozwarte inequality: 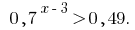
Solutions:
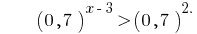
Function
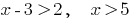
Answer: 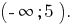
More complex exponential inequalities
With the help of equivalent transformations
With the help of equivalent transformations (scheme the solution of model equations) given inequality reduces to the known inequality of the form (square, fractional or other). After the solution of the resulting inequality we come to the simplest exponential inequalities.
Example 3
Rozwarte inequality: 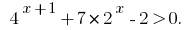
Solutions:
Substitution 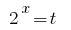 gives the inequality
gives the inequality 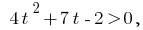
junctions which 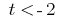 or
or 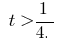
So 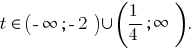
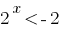 (rozvytku no), or
(rozvytku no), or 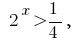 where
where 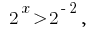 that is
that is 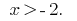
Answer: 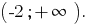
Using the General method of intervals
Apply the General method of intervals,
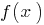
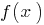 in each of the intervals to which DHS is broken.
in each of the intervals to which DHS is broken.
Example 4
Rozwarte inequality: 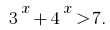
Solutions:
Solve the inequality by the method of intervals. The given inequality weselna bumps 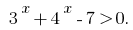
We denote 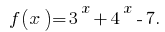
- DHS:
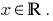
- The zeros of the function:
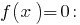
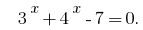
- Because the function
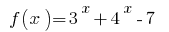 is increasing, the value of zero, it takes only one point of the region definition:
is increasing, the value of zero, it takes only one point of the region definition: - Denote the zero function on DHS, find the sign
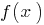 in each of the intervals to which DHS Rotblat, and record the interchange of bumps
in each of the intervals to which DHS Rotblat, and record the interchange of bumps 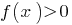
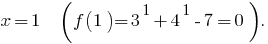
Answer: 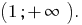
The solution to inequalities is very similar to the model equations, so if You haven't found a suitable Roseanna irregularities, see exponential equations.

 When a > 1
When a > 1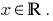
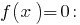
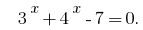
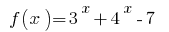 is increasing, the value of zero, it takes only one point of the region definition:
is increasing, the value of zero, it takes only one point of the region definition: