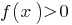Gleichwertiges Umwandlung einfachsten Ungleichungen
 Bei a > 1
Bei a > 1
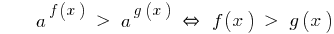
Ein Zeichen der Ungleichheit bleibt.
Beispiel 1
Розвяжіть Ungleichheit: 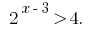
Lösung:
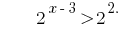
Die Funktion 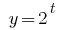 ist mit steigendem somit gleichzusetzen Indikatoren,
ist mit steigendem somit gleichzusetzen Indikatoren,
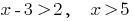
Antwort: 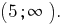
 Bei 0 < a < 1
Bei 0 < a < 1
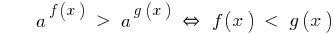
Ein Zeichen der Ungleichheit Umgekehrt.
Beispiel 2
Розвяжіть Ungleichheit: 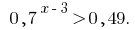
Lösung:
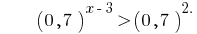
Funktion
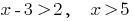
Antwort: 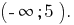
Lösung komplexer exponentielle Ungleichungen
Über gleichwertige Transformationen
Mit Hilfe der gleichwertige Transformationen (nach dem Schema der Lösung exponentielle Gleichungen) festgelegte Ungleichheit kommt es zu Ungleichheiten der bekannten Art (quadratisch, gebrochene oder andere). Nach der Entscheidung der resultierenden Ungleichheit kommen zu den einfachsten exponentielle Ungleichungen.
Beispiel 3
Розвяжіть Ungleichheit: 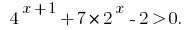
Lösung:
Ersatz 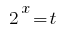 gibt Ungleichheit
gibt Ungleichheit 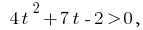
die Entkopplung der 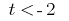 oder
oder 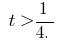
Also 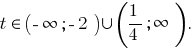
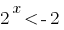 (розвязків nicht) oder
(розвязків nicht) oder 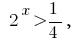 wo
wo 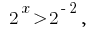 das heißt
das heißt 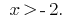
Antwort: 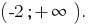
Mit Hilfe der Allgemeinen Methode Intervalle
Wenden wir die Allgemeine Methode der Intervalle,
- Finden DHS
- Eine Funktion Nullen

- Beachten Nullen Funktionen auf DHS und finden Sie die Zeichen
 in jeder der Zwischenräume, in die sich ein DHS.
in jeder der Zwischenräume, in die sich ein DHS. - Antwort schreiben, angesichts der Zeichen der Ungleichheit.
Beispiel 4
Розвяжіть Ungleichheit: 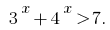
Lösung:
Lösen die Ungleichheit der Methode der Intervalle. VORGEGEBENE Ungleichheit івносильна Unebenheiten 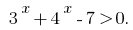
Bezeichnen 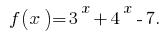
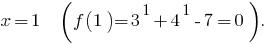
- DHS:
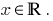
- Nullen Funktionen:
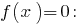
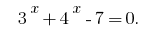
- Da die Funktion
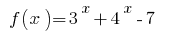 ist mit steigendem, dann ist der Wert gleich null, Sie nimmt nur in einem Punkt Definitionsbereich:
ist mit steigendem, dann ist der Wert gleich null, Sie nimmt nur in einem Punkt Definitionsbereich: - Wir bezeichnen die Nullstellen der Funktion auf der DHS, finden wir das Zeichen
 in jeder der Zwischenräume, die розбвається DHS, und notieren Sie die Ausfahrt Unebenheiten
in jeder der Zwischenräume, die розбвається DHS, und notieren Sie die Ausfahrt Unebenheiten 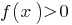
Antwort: 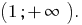
Lösung von Ungleichungen sehr ähnlich bis zu den bezeichnenden Gleichungen, so dass, wenn Sie nicht finden розязання geeigneten Rauhigkeit, gehen Sie auf die Seite von exponential-Gleichungen.

 Bei a > 1
Bei a > 1
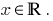
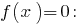
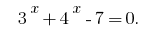
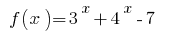 ist mit steigendem, dann ist der Wert gleich null, Sie nimmt nur in einem Punkt Definitionsbereich:
ist mit steigendem, dann ist der Wert gleich null, Sie nimmt nur in einem Punkt Definitionsbereich: