Definition: eine Gleichung mit einer Variablen 
— diese Gleichung mit einer Variablen 
, die in der Allgemeinen Form wird so geschrieben: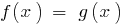 
Definition: die Wurzel (oder розвязком) Gleichungen nennt man den Wert der Variablen, welche aus der Gleichung in die richtige numerische Gleichheit.
Розвязати Gleichungen — dann finden Sie alle Ihre Wurzeln (Entkopplung) oder zeigen, dass Sie es nicht sind.
Der Bereich der zulässigen Werte (DHS) Gleichungen
Definition: der Bereich der zulässigen Werte (das Gebiet) der Gleichung — Bereich Allgemeine Definitionen für Funktionen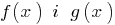 
, die im linken und rechten Teil der Gleichung.
Suchen Sie den Bereich der zulässigen Werte (DHS)
Beispiel
Definiert die Gleichung: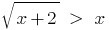 
DHS: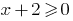 
, D. H. 
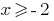, da der Bereich der Definition der Funktion 
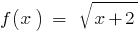bestimmt durch die Bedingung 
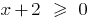, und der Bereich der Definition der Funktion 
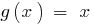ist die Menge aller reellen zahlen.
Gleichungen — Untersuchung
Wenn jede Wurzel der ersten Gleichung ist die Wurzel der zweiten Gleichung, so ist die zweite Gleichung nennt man eine Folge der ersten Gleichung.
Wenn von der Richtigkeit der ersten Gleichheit folgt die Richtigkeit jeder der folgenden, одержумо Gleichung—Folge
Daher ist bei der Verwendung der Gleichungen—Prüfung der erzielten Wirkungen indem Sie Wurzeln in der ursprünglichen Gleichung ist Bestandteil der Lösung.
Beispiel 1
Розвязати Gleichungen: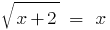 
Lösung:
Hätten ja beide Teile der Gleichung im Quadrat:
;
;
;
.
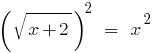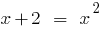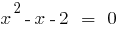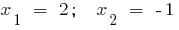Machen Sie eine überprüfung.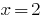 
— Wurzel 
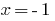— fremde Wurzel.
Antwort: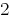 
.
Gleichwertiges Gleichungen
Definition: Gleichwertiges (äquivalente) Gleichungen zwei Gleichungen, die auf einer Vielzahl von DHS haben die gleiche Auflösung, das heißt jede Lösung der ersten Gleichung ist розвязком der zweiten und Umgekehrt.
Einige Theoreme über равносильности Gleichungen
Theorem 1: Wenn von einem Teil der Gleichungen verschieben in einen anderen Teil des Summanden mit umgekehrtem Vorzeichen, so erhalten wir die Gleichung, was gleichbedeutend ist mit dem angegebenen (auf einer beliebigen Menge).
Theorem 2: Wenn beide Teile der Gleichung multiplizieren oder dividieren auf die gleiche Zahl, die nicht gleich null sind (oder auf dieselbe Funktion, die definiert und nicht null auf der DHS angegebenen Gleichung), dann erhalten wir die Gleichung, was gleichbedeutend ist mit dem angegebenen.
Theorem 3: Wenn die beiden Teile der Gleichung 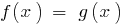nehmen wachsende (oder fallende) Funktion 
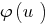und dabei nicht відбувється Verengung der DHS angegebenen Gleichung 
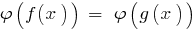wird was gleichbedeutend ist mit dem angegebenen ( DHS).
Untersuchung der Theoreme über равносильности Gleichungen
Folge: Da die Funktion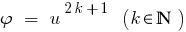 
monoton Steigend,dann
.
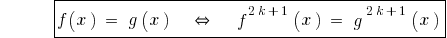Bei der überreichung der beiden Teile der Gleichung in ungeraden natürlichen Grad erhalten wir eine Gleichung, was gleichbedeutend ist mit dieser.
Folge: Da die Funktion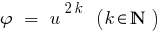 
nur monoton Steigend, wenn 
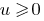,im Falle, wenn beide Teile der Gleichung невідємні, beim heben beider Teile bis zu einer geraden natürlichen Grad erhalten wir eine Gleichung, was gleichbedeutend ist mit dieser.