Das Konzept der umgekehrten Funktion: Lassen Sie die Funktion  nimmt jeder seinen Wert in dem einzigen Punkt Ihrer Definitionsbereich (eine solche Funktion nennt man reversibel ). Dann zu jeder Zahl
nimmt jeder seinen Wert in dem einzigen Punkt Ihrer Definitionsbereich (eine solche Funktion nennt man reversibel ). Dann zu jeder Zahl  ( aus einer Menge der Funktionswerte
( aus einer Menge der Funktionswerte  ) es ist der einzige Wert
) es ist der einzige Wert  (aus dem Definitionsbereich der Funktion
(aus dem Definitionsbereich der Funktion  ), ist, dass
), ist, dass 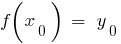 . Betrachten wir eine neue Funktion
. Betrachten wir eine neue Funktion 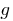 , die jede Zahl
, die jede Zahl  stellt in übereinstimmung der Zahl
stellt in übereinstimmung der Zahl  , dh
, dh 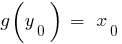 . In diesem Fall wird die Funktion
. In diesem Fall wird die Funktion 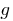 namens Reverse - Funktion
namens Reverse - Funktion  .
.
Eigenschaften Umkehrfunktionen
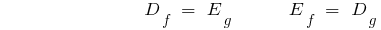
- Das Gebiet der geraden Funktionen ist eine Vielzahl von Werten Backlink, sondern eine Vielzahl von Werten Luftlinie Funktionen - das Gebiet der Bestimmung der inversen.
- Wenn die Funktion steigt (sinkt) auf einem gewissen Intervall, und es hat die umgekehrte Funktion auf diesem Intervall, die wächst, wenn eine direkte Funktion zunimmt, und abnimmt, wenn eine direkte Funktion kommt.
- Grafik-und Rücklauf-Funktionen sind symmetrisch bezüglich der geraden
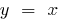 (die Winkelhalbierende des ersten und Dritten Achsen-Winkel)
(die Winkelhalbierende des ersten und Dritten Achsen-Winkel)
Auch die umgekehrte Funktionen
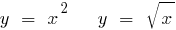
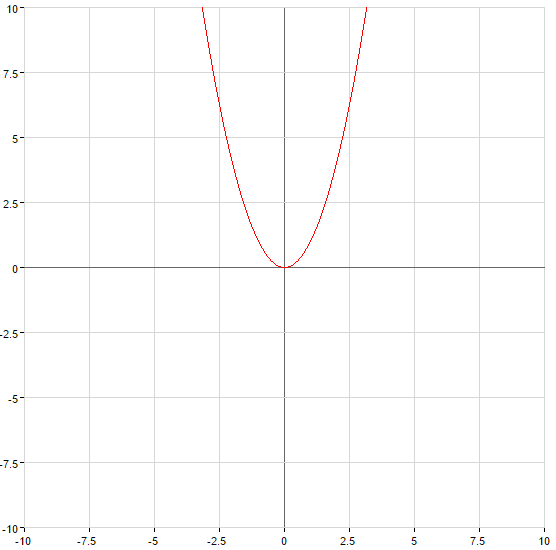
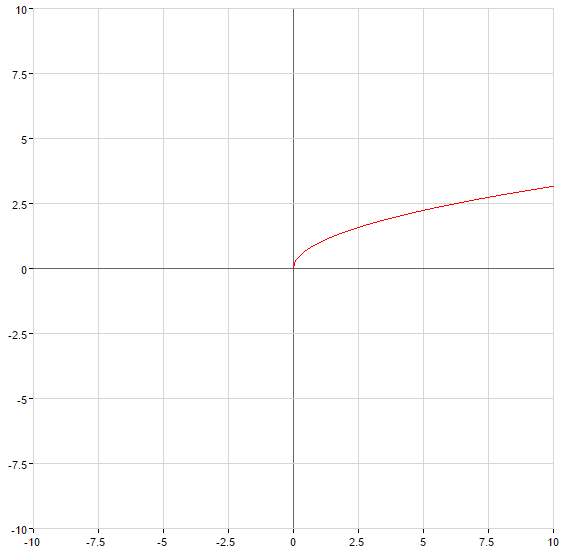
Ein Beispiel für den Verbleib der umgekehrten Funktion
Beispiel: Eine umkehrfunktion für die Funktionen: 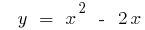
Lösung: wo Finden die angegebene Funktion steigt und schwindet 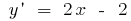 . Dann
. Dann 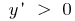 , wenn
, wenn 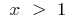 die Funktion steigt
die Funktion steigt 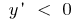 , wenn
, wenn 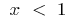 die Funktion nachläßt.
die Funktion nachläßt.
Auf jedem dieser Zwischenräume 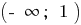 und
und 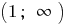 schreiben wir die Formel der umgekehrten Funktion. Weil
schreiben wir die Formel der umgekehrten Funktion. Weil 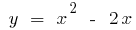 , dann
, dann 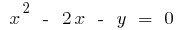 .
.
Von hier aus 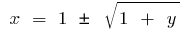 , D. H. wenn
, D. H. wenn 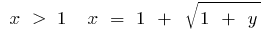 , und wenn
, und wenn 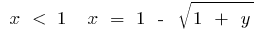 . Ändert die Bezeichnung auf die traditionelle, erhalten wir für die Funktion
. Ändert die Bezeichnung auf die traditionelle, erhalten wir für die Funktion 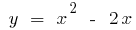 bei der
bei der 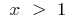 Reverse-Funktion wird die Funktion
Reverse-Funktion wird die Funktion 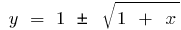 , und beim
, und beim 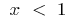 Reverse-Funktion wird die Funktion
Reverse-Funktion wird die Funktion 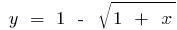 .
.

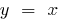 (die Winkelhalbierende des ersten und Dritten Achsen-Winkel)
(die Winkelhalbierende des ersten und Dritten Achsen-Winkel)