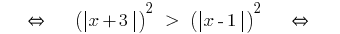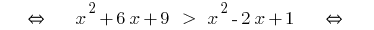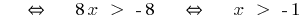Definition: Ungleichheit mit einer Variablen 
zwei Ausdrücke mit Variablen eine Vereinigte mit Vorzeichen, 
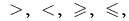die in der Allgemeinen Form wird so geschrieben: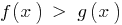 
Definition: die Wurzel (oder розвязком) Ungleichheit wird als Wert der Variable, welche aus der Ungleichheit in die richtige numerische Gleichheit.
Розвязати Ungleichheit — dann finden Sie alle Ihre Wurzeln (Entkopplung) oder zeigen, dass Sie es nicht sind.
Der Bereich der zulässigen Werte DHS Ungleichheit
Definition: der Bereich der zulässigen Werte (area Definition) Ungleichmäßigkeit — Bereich Allgemeine Definitionen für Funktionen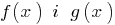 
, die im linken und rechten Teil der Gleichung.
Suchen Sie den Bereich der zulässigen Werte (DHS)
Beispiel
Definiert die Gleichung: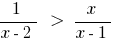 
DHS: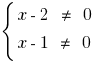 
, D. H.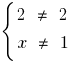 
, was kann man aufnehmen und so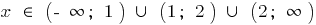 
.
Die Ungleichmäßigkeit — Folgen
Bei розвязувнні Unebenheiten Folgen werden nicht verwendet (und verwendet gleichwertiges Umwandlung), da in der Regel nicht Scannen alle erhaltenen розвязків Ungleichheit-Untersuchung.
Gleichwertiges Ungleichungen
Definition: Äquivalent (gleichwertig) Unebenheiten — zwei Unebenheiten, die auf einer Vielzahl von DHS haben die gleiche Auflösung, das heißt, jede Entscheidung der ersten Ungleichheit ist розвязком zweite und Umgekehrt.
Einige Theoreme über равносильности Gleichungen
Theorem 1: Wenn von einem Teil der Ungleichheit verschieben in einen anderen Teil des Summanden mit umgekehrtem Vorzeichen, so erhalten wir нерівнсть, was gleichbedeutend ist mit dem angegebenen (auf einer beliebigen Menge).
Theorem 2.1: Wenn beide Teile Ungleichungen multiplizieren oder dividieren auf die gleiche positive Zahl ungleich null (oder auf dieselbe Funktion, die definiert und nicht null auf der DHS angegebenen Gleichung), so bekommen wir die Ungleichheit was gleichbedeutend ist mit dem angegebenen.
Theorem 2.2: Wenn beide Teile Ungleichungen multiplizieren oder dividieren auf dasselbe відємне Zahl, die nicht gleich null sind (oder auf dieselbe Funktion, die definiert und відємна auf DHS angegebenen Gleichung) und, ASO, tauschen Zeichen der Ungleichheit auf der gegenüberliegenden Seite, dann bekommen wir die Ungleichheit, was gleichbedeutend ist mit dem angegebenen.
Theorem 3.1: Wenn von beiden teilen Ungleichheit 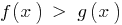nehmen Sie eine zunehmende Funktion 
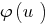(speichern Sie ein Zeichen der Ungleichheit), dabei geschieht die Verengung der DHS angegebenen Ungleichungen, das resultierende Ungleichheit 
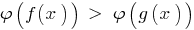wird gleichbedeutend mit dem angegebenen ( DHS).
Theorem 3:2 Wenn von beiden teilen Ungleichheit 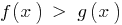nehmen fallende Funktion 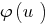, indem Sie das Zeichen der Ungleichheit, und dabei geschieht die Verengung der DHS angegebenen Ungleichungen, das resultierende Ungleichheit 
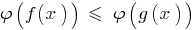wird gleichbedeutend mit dem angegebenen ( DHS).
Untersuchung der Theoreme über равносильности Ungleichungen
Folge: Da die Funktion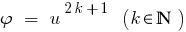 
monoton Steigend,dann
.
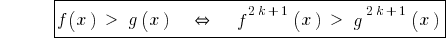Bei der überreichung der beiden Teile bis zu einer ungeraden natürlichen Grad bekommen Ungleichheit, was gleichbedeutend ist mit dieser.
Folge: Da die Funktion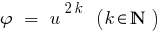 
nur monoton Steigend, wenn 
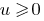,im Falle, wenn beide Teile der Ungleichheit невідємні, beim heben beider Teile bis zu einer geraden natürlichen Grad bekommen нерінвість, was gleichbedeutend ist mit dieser.
Beispiel 1
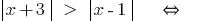(beide Teile невідємні!)
