Definition:Wenn die Funktion 
definiert auf der Strecke 
und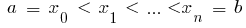 
dann bestimmte интегралом von Funktionen auf einem Intervall nennt man eine Zahl, die die Grenze der integrierten Beträge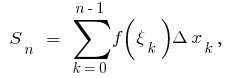 
wo 
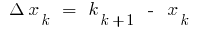, f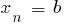 
das heißt
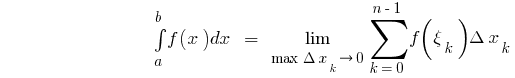
wo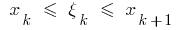 
i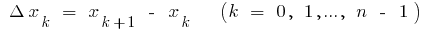 
Der Aufbau der integrierten Summe am Beispiel der Bestimmung der gekrümmten Fläche des Trapezes
Lassen Sie sich auf ein Segment festgelegt неотъемлемою und eine kontinuierliche Funktion
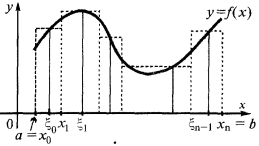
Um zur Bestimmung der Fläche des krummlinigen Trapezes (begrenzte Kurve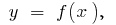 
der Achse 
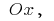und den geraden, 
und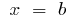 
), brechen Schnitt Punkten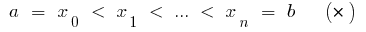 
auf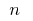 
teilen, wählen Sie auf jedem der empfangenen partiellen Schnitte 
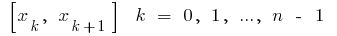beliebigen Punkt 
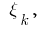berechnen wir die Werte
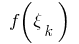der Funktion in diesen Punkten und bilden die Summe 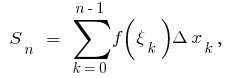wo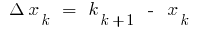
Dieser Betrag entspricht der Summe der Flächen der schraffierten Rechtecken und wird als IC Summe.
Wenn nun die Anzahl der Punkte Gruppenwechsel unbegrenzt erhöht und die Länge der maximalen (größten) teilweise geschnittene Gruppenwechsel gegen null geht, und dabei der Wert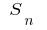 
neigt zu einer gewissen Grenze 
unabhängig von der Art der Partitionierung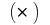 
und Auswahl der Punkte 
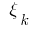auf Teil Strecken, dann den Wert 
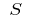nennen der gekrümmten Fläche des Trapezes, D. H.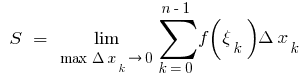 
Die Formel Von Newton - Leibniz
Wenn die Funktion definiert ist und kontinuierlich auf der Strecke und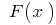 
Ihre primitive (D. H. 
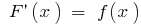), dann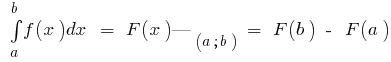 
Beispiel. Da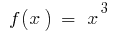 
eine der primitiven 
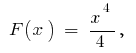ist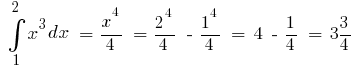 
Grundlegende Eigenschaften bestimmter Integrale
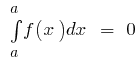
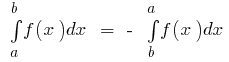
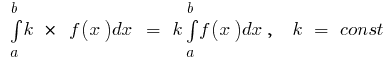
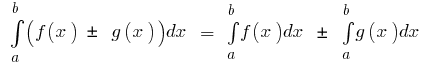
- Wenn
integrierte auf 
und 
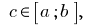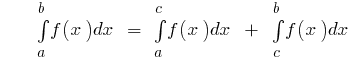
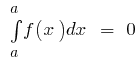
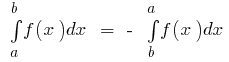
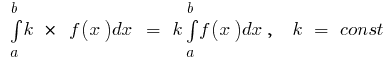
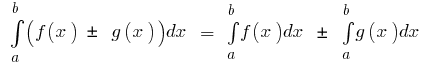
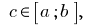dann
dann