Das Konzept der irrationalen Gleichung
Definition: eine Irrationale Gleichung 
— Gleichung, die eine Variable unter dem Zeichen der Wurzel -Klasse.
Lösung von irrationalen Gleichungen
Bei der überreichung der beiden Teile der Gleichung den Grad der ungeraden (1,3,5,7....) wir erhalten eine Gleichung, was gleichbedeutend ist mit dem angegebenen (auf ihn DHS)
Beispiel 1:
Розвяжіть Gleichungen: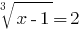 
Lösung: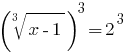 
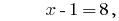
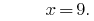
Antwort: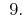
Bei der überreichung der beiden Teile der Gleichung in frischer степеня (2,4,6,8....) auftreten können fremde Wurzeln, die отсеют Kontrolle.
Beispiel 2:
Розвяжіть Gleichungen: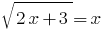 
Lösung: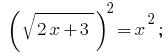 
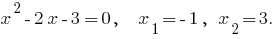
Überprüfung: Beim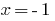 
haben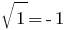 
- eine falsche Gleichheit, also 
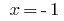- fremde Wurzel.
Bei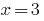 
haben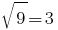 
- die richtige Gleichung und folglich 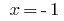- die Wurzel der angegebenen Gleichung.
Antwort: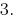
Wenn in der Gleichung die Variable ist in der gleichen Form, зучно die entsprechenden Ausdruck mit einer Variable mit einem Buchstaben bezeichnen (neue Variable).
Beispiel 3:
Розвяжіть Gleichungen: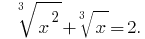 
Lösung: Wir Bezeichne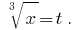n 
Dann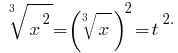 
Wir erhalten die Gleichung: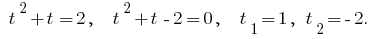 
Führen Feed-Ersatz: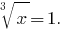 
Dann 
oder 
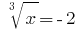hier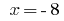 
.
Bei 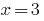haben 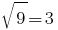- die richtige Gleichung und folglich 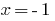- die Wurzel der angegebenen Gleichung.
Antwort: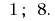
- Durch heben beider Teile irrationalen Gleichungen auf einer Stufe
- Über den Austausch von Variablen