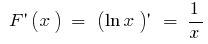Original
Definition:eine Funktion 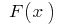 heißt von der ursprünglichen Funktion
heißt von der ursprünglichen Funktion  auf diesem Intervall, wenn für alle
auf diesem Intervall, wenn für alle  aus dieser Lücke
aus dieser Lücke 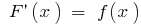
Beispiele
- Für die Funktion
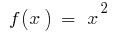 auf dem Intervall
auf dem Intervall 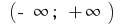 ursprünglichen ist
ursprünglichen ist 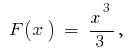 da
da 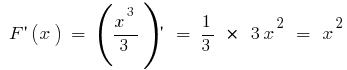
- Für die Funktion
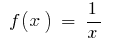 auf dem Intervall
auf dem Intervall 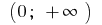 ursprünglichen ist
ursprünglichen ist 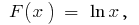 da
da 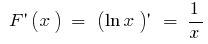
Die wichtigste Eigenschaft первообразных
Wenn die Funktion 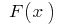 ist die ursprüngliche Funktion
ist die ursprüngliche Funktion  auf diesem Intervall, und
auf diesem Intervall, und 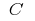 — eine willkürliche Konstante, gibt die Funktion
— eine willkürliche Konstante, gibt die Funktion 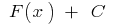 auch ist die ursprüngliche Funktion
auch ist die ursprüngliche Funktion 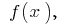 dabei jede primitive Funktion
dabei jede primitive Funktion  auf diesem Intervall kann geschrieben werden als
auf diesem Intervall kann geschrieben werden als 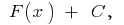 wo
wo 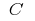 — willkürliche geworden
— willkürliche geworden
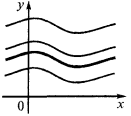
Geometrische Bedeutung
Alle Grafiken первообразных dieser Funktion ergeben sich aus einander parallele übertragung entlang der Achse 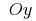
Unbestimmte Integral
Definition:die Gesamtheit aller первообразных diese Funktion  wird als ungewiss интегралом und gekennzeichnet durch
wird als ungewiss интегралом und gekennzeichnet durch 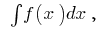 dh
dh 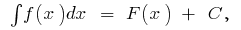 wo
wo 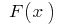 eine первообразных Funktionen
eine первообразных Funktionen 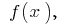 und
und 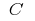 — etwas geworden ist
— etwas geworden ist
Die Regeln der Integration
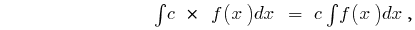 wo
wo 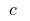 — war
— war
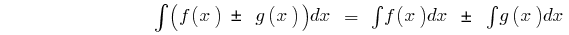
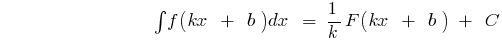

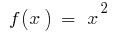 auf dem Intervall
auf dem Intervall 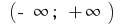 ursprünglichen ist
ursprünglichen ist 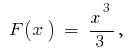 da
da 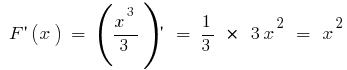
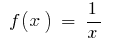 auf dem Intervall
auf dem Intervall 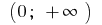 ursprünglichen ist
ursprünglichen ist 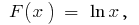 da
da