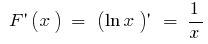Первоначальная
Определение: Функция 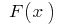 называется первоначальной для функции
называется первоначальной для функции  на данном промежутке, если для любых
на данном промежутке, если для любых  из этого промежутка
из этого промежутка 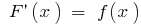
Примеры
- Для функции
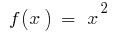 на интервале
на интервале 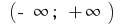 первоначальной является
первоначальной является 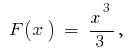 поскольку
поскольку 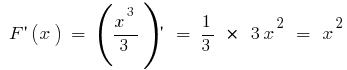
- Для функции
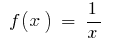 на интервале
на интервале 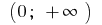 первоначальной является
первоначальной является 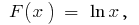 поскольку
поскольку 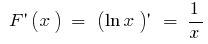
Основное свойство первообразных
Если функция 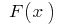 является первоначальной для функции
является первоначальной для функции  на данном промежутке, а
на данном промежутке, а 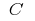 — произвольная постоянная, то функция
— произвольная постоянная, то функция 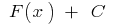 также является первоначальной для функции
также является первоначальной для функции 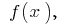 при этом любая первообразная для функции
при этом любая первообразная для функции  на данном промежутке может быть записана в виде
на данном промежутке может быть записана в виде 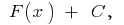 где
где 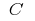 — произвольная стала
— произвольная стала
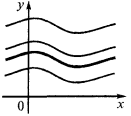
Геометрический смысл
Графики любых первообразных данной функции получаются друг из друга параллельным переносом вдоль оси 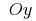
Неопределенный интеграл
Определение:Совокупность всех первообразных данной функции  называется неопределенным интегралом и обозначается символом
называется неопределенным интегралом и обозначается символом 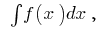 т. е.
т. е. 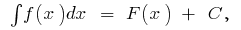 где
где 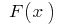 — одна из первообразных функций
— одна из первообразных функций 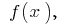 а
а 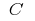 — некоторая стала
— некоторая стала
Правила интегрирования
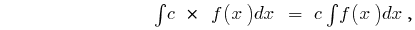 где
где 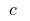 — стала
— стала
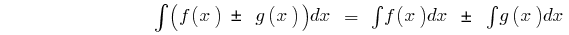
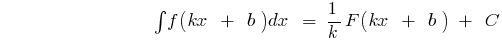

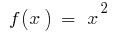 на интервале
на интервале 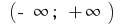 первоначальной является
первоначальной является 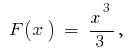 поскольку
поскольку 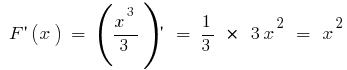
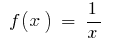 на интервале
на интервале 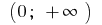 первоначальной является
первоначальной является 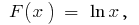 поскольку
поскольку