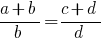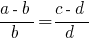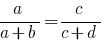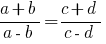Пропорции и отношения, прямая и обратная пропорциональность

Определение: Пропорцией называется равенство двух отношений.

или .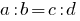

Основное свойство пропорций

Произведение крайность членов членов пропорции равно произведению ее средних членов: если

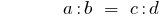, то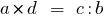

Свойства пропорций

1. Произведение крайность членов членов пропорции равно произведению ее средних членов: .
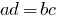2. Каждый крайний член пропорции равен произведению ее средних членов, деленному на другой крайний член.
3. В каждой пропорции можно поменять местами или только средние члены или крайние, или и те, и другие одновременно.

Пример нахождения пропорции в математике

Если 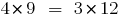, то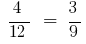

В пропорции 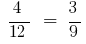изменим местами средние члены или крайние члены, тогда получим опять правильные равенства:

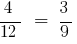и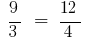

Производные пропорции

Если заданная пропорция 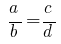, то 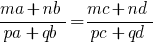, что называется производной пропорцией.

Наиболее часто употребляемые производные пропорции

• 
• 
• 
• 

Масштаб

Определение: Масштаб — отношение расстояния на карте к соответствующему расстоянию на реальной местности.

Прямо пропорциональные величины

Определение: Две величины называются прямо пропорциональными, если с увеличением значений одной из них в несколько раз значение другой увеличивается во столько же раз.

Задачи на прямо пропорциональные величины

Сторона квадрата равна 3 дм. Как изменится периметр квадрата, если его сторону увеличить в 3 раза, в 4 раза, в 5 раз?

Сторона квадрата 3 дм, периметр 12 дм

Сторона квадрата 9 дм, периметр 36 дм

Сторона квадрата 12 дм, периметр 48 дм

Сторона квадрата 15 дм, периметр 60 дм

При увеличении стороны квадрата в 3 раза (была 3 дм, стала — 9 дм), периметр увеличился также в 3 раза (был 9 дм, стал — 36 дм).

Аналогично, при увеличении стороны квадрата в 4 раза (была 3 дм, стала — 12 дм), периметр увеличился также в 4 раза (был 12 дм, стал — 48 дм).

Вывод: при увеличении стороны квадрата в несколько раз, периметр увеличивается во столько же раз.

Сторона квадрата прямо пропорциональна его периметру.

Обратно пропорциональные величины

Определение: Две величины называются обенено пропорциональными, если с увеличением значений одной из них в несколько раз значение другой уменьшается во столько же раз.

Задачи на обратно пропорциональные величины

Расстояние между двумя поселками равно 160 км. За какое время можно доехать из одного поселка в другой, если скорость 10 км/ч увеличить в 2 раза, 4 раза, в 8 раз?

Скорость, км/ч 10 время, ч 16

Скорость, км/ч 20 время, ч 8

Скорость, км/ч 40 время, ч 4

Скорость, км/ч 80 время, ч 2

При увеличении скорости в 2 раза (была 10 км/ч, стала — 20 км/ч), время сократился (уменьшился) в 2 раза (было 16 ч, стало — 8 ч).

Аналогично, при увеличении скорости в 4 раза (была 10 км/ч, стала — 40 км/ч), время сократился (уменьшился) в 4 раза (было 16 ч, стало — 4 ч).

Вывод: при увеличении скорости в несколько раз, время уменьшается во столько же раз.

Скорость обратно пропорциональна времени.

Числа 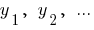пропорциональные числам 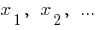, если 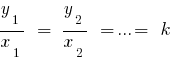— коэффициент пропорциональности.
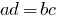