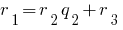Определение: Наибольшим общим делителем двух или нескольких натуральных чисел называют наибольшее натуральное число, на которое делится каждое из данных чисел.
Например
НОД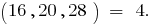
Взаимно простые числа
Определение: Два натуральных числа называются взаимно простыми, если их НОД равен единице.
Нахождение НОД с помощью разложения на простые множители
Чтобы найти НОД двух или нескольких чисел, необходимо:
- Разложить данные числа на простые множители.
- Составить произведение из общих простых множителей, взятых с наименьшим показателем степени.
- Найти значение произведения.
Алгоритм Евклида
- Поделить
 на
на  с остачею:
с остачею: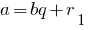
- Разделить делитель
 на
на 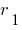 :
: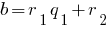
- Разделить делитель
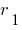 на новую остаток
на новую остаток 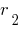 :
: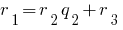
Последняя отличная от нуля остаток и есть НОД.
Наименьшее общее кратное (НОК)
Наименьшим общим кратным двух или нескольких натуральных чисел называют наименьшее натуральное число, которое делится на каждое из данных чисел.
Нахождение нок двух натуральных чисел
Чтобы найти нок двух или нескольких чисел, необходимо:
HCK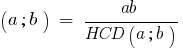
Например
НСК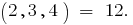
Связь между НОД и нок двух чисел
НОД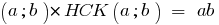

 на
на  с остачею:
с остачею: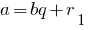
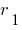 :
: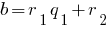
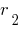 :
: