Десятичные дроби

Десятичная дробь — дробь, знаменатель которого 10ⁿ, где n — натуральное число.

Записан десятичная дробь читается согласно схемы

1	2	3	4	,	5	6	7	8
тысячи	сотни	десятки	единицы		десятые	сотые	тысячные	десятитысячные

Например десятичная дробь 10,436 читается "десять целых четыреста тридцать шесть тысячных".

Среди дробей наиболее часто употребляемыми в повседневной жизни есть дроби со знаменателями 10, 100, 1000 и т.д.

Например, 10 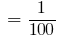г кг,

1м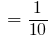м см,

2см 5мм 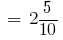см и т.д.

Числа со знаменателями 10, 100, 1000 и т. д. договорились записывать без знаменателя.
Сначала пишут целую часть, а потом числитель дробной части. Целую часть отделяют от дробной части запятой.

Например, вместо 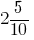пишут 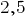(читают: «2 целых и 5 десятых»).

Любое число, знаменатель дробной части которого выражается единицей с одним или несколькими нулями, можно представить в виде десятичного дроби.

Если дробь правильная, то перед запятой пишут цифру 0.
Например, вместо 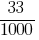пишут 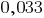(читают: «0 целых и 33 тысячная»).

Обрати внимание! После запятой числитель дробной части должен иметь столько же цифр, сколько нулей в знаменателе.

Таблица разрядов десятичных дробей

Десятичная дробь, как и любое число, состоит из цифр (0,1,2,3,4,5,6,7,8,9).

Место каждой цифры в числе важное: оно определяет разряд числа.

Десятичная дробь состоит из целой части (все цифры до запятой) и дробной части (все цифры после запятой).

Целую часть десятичной дроби можно разбить на разряды также, как и натуральные числа: единицы, десятки, сотни, тысячи и т. д.

Дробная часть десятичной дроби разбивают на разряды так: десятые (в знаменателе обыкновенной дроби 10), сотые (десятые (в знаменателе обыкновенной дроби 100), тысячные (десятые (в знаменателе обыкновенной дроби 1000) и т.д.

Таблицу разрядов можно дополнить любым нужным количеством столбцов.

1. 1-й разряд после запятой — разряд десятых,
2. 2-й разряд после запятой — разряд сотых,
3. 3-й разряд после запятой — разряд тысячных,
4. 4-й разряд после запятой — разряд десятитысячных,
5. 5-й разряд после запятой — разряд стотысячных,
6. 6-й разряд после запятой — разряд миллионных,
7. 7-й разряд после запятой — разряд десятимиллионным,
8. 8-й разряд после запятой — разряд стомільйонних.

Сложение и вычитание десятичных дробей

Чтобы добавить или вычесть десятичные дроби, нужно:

1. Уравнять в этих дробях количество знаков после запятой;
2. Записать их друг под другом так, чтобы запятая была записана под запятой;
3. Выполнить сложение (вычитание), не обращая внимания на запятую;
4. Поставить в ответе запятую под запятой в данных дробях.

Пример:

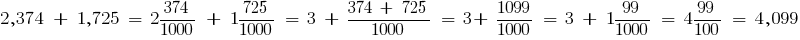
Свойства сложения для десятичных дробей:

a + b = b + a - переставная свойство

(a + b) + c = a + ( b + c ) - связующее свойство

Умножение десятичных дробей

Чтобы перемножить две десятичные дроби, надо:
1. выполнить умножение, не обращая внимания на запятые;
2. отделить запятой столько цифр справа, сколько их после запятой в обоих множителях вместе.

Подробнее читайте здесь

Деление десятичных дробей

Чтобы поделить десятичную дробь на натуральное число, надо:
1. разделить дробь на это число, не обращая внимания на запятую;
2. поставить в частном запятую, когда закончится делення целой части.

Подробнее читайте здесь

Сравнение десятичных дробей

Чтобы сравнить две десятичные дроби, надо сначала уравнять у них число десятичных знаков, приписав к одной из них справа нули, а потом, отбросив запятую, сравнить получившиеся натуральные числа.

Пример:

Сравним две десятичные дроби 0,642 и 0,65. Уравняем число десятичных знаков, приписав к числу 0,65 дело ноль. Получим дроби 0,564 и 0,650.

Запишем их в виде обыкновенных дробей:

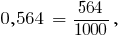
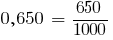
Знаменатели дробей одинаковы.

Из двух дробей с одинаковыми знаменателями, больше то дробь, который имеет больший числитель.
Так как 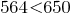, то 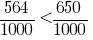, а следовательно,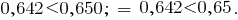

Десятичные дроби можно сравнивать и по разрядам.

В десятичных дробях 26,63 и 6,553 достаточно сравнить целые части. Так как 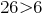, то и ;.

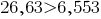Конечные и бесконечные десятичные дроби

Определение:Конечным десятичной дробью называется дробь, который содержит конечную количество цифр после запятой.

Пример: 222,35

Определение: Бесконечной десятичной дробью называется дробь, который не содержит конечной количества цифр после запятой.

Пример: 222,35...

Определение:Бесконечным периодическим десятичным числом (периодическим дробью) называется бесконечный дробь, в конце содержит группу цифр, которые повторяются.

Пример: 222,489898989...

Периодом бесконечной периодической десятичной дроби называется группа цифр, которые повторяются. В предыдущем примере-это 89.

Периодическая десятичная дробь называется чистой периодической дробью, если ее период начинается сразу после запятой, а период может содержать любое конечное число цифр.

Пример: 8,44444....

Периодическая десятичная дробь называется смешанной дробью, если периодическая десятичная дробь содержит еще число, помещенное между целой частью и периодом. Число периодической дроби, стоящее между целой частью и периодом, называется передперіодом этой дроби.

Пример: 8,4578787878...