Монотонность и постоянство функции
Достаточное условие возрастания функции
Если в каждой точке интервала 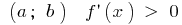 , то функция возрастает на этом интервале
, то функция возрастает на этом интервале
Достаточное условие убывания функции
Если в каждой точке интервала 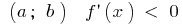 , то функция убывает на этом интервале
, то функция убывает на этом интервале
Замечание. Эти условия являются лишь достаточными, но не являются необходимыми условиями роста и убывания функции
Необходимое и достаточное условие постоянства функции
Функция  является постоянной на интервале
является постоянной на интервале 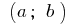 тогда и только тогда, когда
тогда и только тогда, когда  во всех точках всего интервала
во всех точках всего интервала
Экстремумы (максимумы и минимумы) функции
Точка максимума
Определение: Точка  из области определения функции
из области определения функции  называется точкой максимума этой функции, если найдется
называется точкой максимума этой функции, если найдется 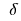 - окрестность
- окрестность 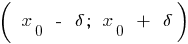 точки
точки  , что для всех
, что для всех 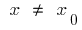 из этой окрестности выполняется неравенство
из этой окрестности выполняется неравенство 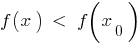
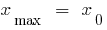 — точка максимума
— точка максимума
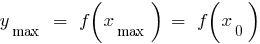 — максимум
— максимум
Точка минимума
Определение: Точка  из области определения функции
из области определения функции  называется точкой минимума этой функции, если найдется
называется точкой минимума этой функции, если найдется 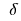 - окрестность
- окрестность 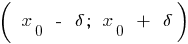 точки
точки  , что для всех
, что для всех 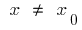 из этой окрестности выполняется неравенство
из этой окрестности выполняется неравенство 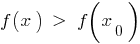
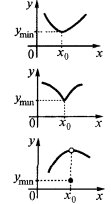
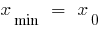 — точка минимума
— точка минимума
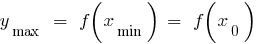 — минимум
— минимум
Критические точки
Определение: Внутренние точки области определения функции, в которых производная функции равна нулю или не существует, называются критическими
Необходимое условие экстремума
 — точка экстремума
— точка экстремума 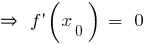 или
или 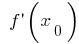 — не существует
— не существует
(но не в каждой точке  , где
, где 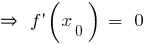 или
или 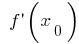 не существует, будет экстремум!)
не существует, будет экстремум!)
Достаточное условие экстремума
в точке  знак
знак 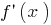 меняется с
меняется с 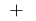 на
на 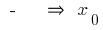 — точка максимума
— точка максимума
в точке  знак
знак 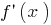 меняется с
меняется с 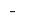 на
на 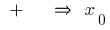 — точка минимума
— точка минимума
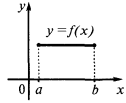
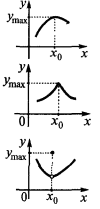
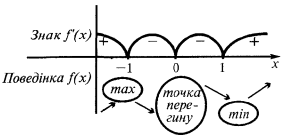
Пример графика функции  , что имеет экстремумы
, что имеет экстремумы
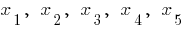 — критические точки
— критические точки
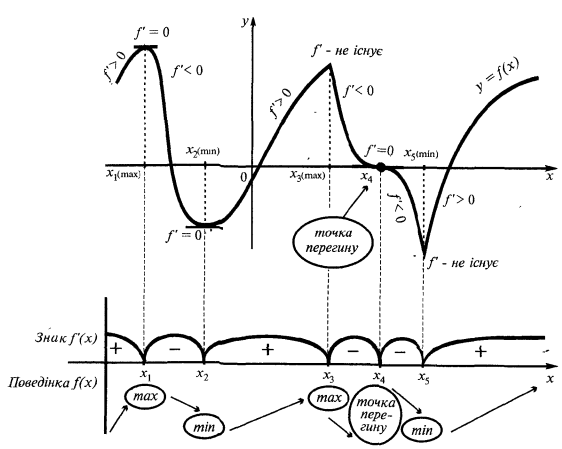
Исследование функции на монотонность и экстремумы
- Найти область определения и интервалы, на которых функция непрерывна
- Найти производную

- Найти критические точки, т. е. внутренние точки области определения, в которых
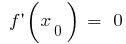 или не существует
или не существует - Обозначить критические точки на области определения, найти знак производной и характер поведения функции на каждом интервале, на которые разбивается область определения
- Относительно каждой критической точки определить, является ли она точкой максимума или минимума или не является точкой экстремума
- Записать потріний результат исследования (промежутки монотонности и экстремумы)
Пример. 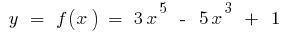
Область определения: 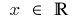
Функция непрерывная в каждой точке своей области определения
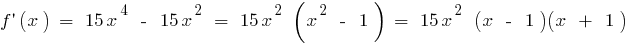
 существует на всей области определения
существует на всей области определения
 при
при 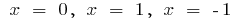
 возрастает при
возрастает при 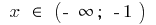 и при
и при 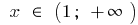
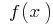 спадает при
спадает при 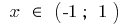
Точки экстремума: 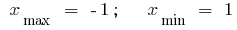
Экстремумы: 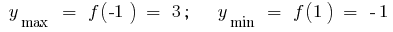
Наибольшее и наименьшее значения функции, непрерывной на отрезке
Свойство: Если функция  непрерывна на отрезке и имеет на нем конечное число критических точек, то она приобретает своего наибольшего и наименьшего значения на этом отрезке либо в критических точках, принадлежащих этому отрезку, либо на концах отрезка
непрерывна на отрезке и имеет на нем конечное число критических точек, то она приобретает своего наибольшего и наименьшего значения на этом отрезке либо в критических точках, принадлежащих этому отрезку, либо на концах отрезка
Нахождение наибольшего и наименьшего значения функции, непрерывной на отрезке
- Найти производную

- Найти критические точки (
 или не существует)
или не существует) - Выбрать критические точки, которые принадлежат заданному отрезку
- Вычислить значения функции в критических точках и на концах отрезка
- Сравнить полученные значения и выбрать из них наименьшее и наибольшее
Пример. 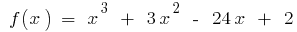 при
при 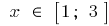
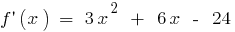
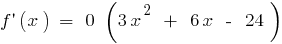 при
при 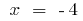 и при
и при 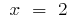
Заданному отрезку 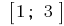 принадлежит лишь критическая точка
принадлежит лишь критическая точка 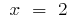
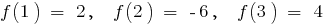


 , что имеет экстремумы
, что имеет экстремумы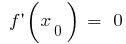 или не существует
или не существует