Пример. 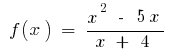
- Область определения
- Четность, нечетность, периодичность
- Пересечение с осями координат
- Производная и критические точки
- Промежутки возрастания, убывания и точки экстремума (и значения функции в этих точках)
- Поведение функции на концах области определения и асимптоты графика функции (вертикальные, горизонтальные и наклонные)
При
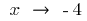 слева
слева 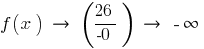
При
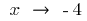 дело
дело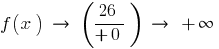
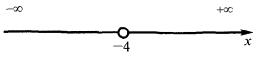
Следовательно,
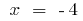 — вертикальная асимптота
— вертикальная асимптотаПоскольку
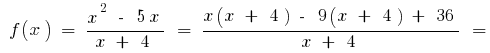
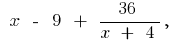 то при
то при 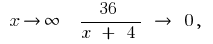 тогда
тогда 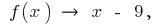 т. е.
т. е. 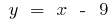 — наклонная асимптота
— наклонная асимптота - Вторая производная и исследование функции на выпуклость и угнутість
- Если необходимо найти контрольные точки, уточняющие поведение графика
- На основе проведенного исследования строим эскиз графика функции
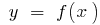
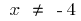
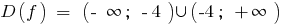
Функция ни четная, ни нечетная и периодическая
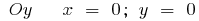
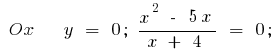
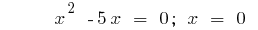 или
или 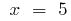
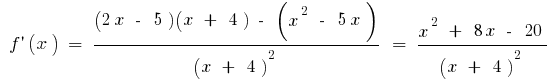
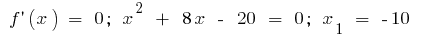 или
или 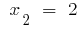
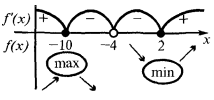
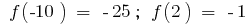
Найти точки перегиба (если они существуют) и значения  в точках перегиба
в точках перегиба
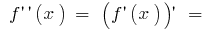
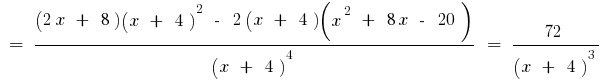
Так 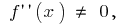 то знак второй производной может меняться только в точке
то знак второй производной может меняться только в точке 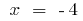
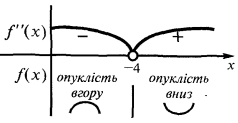
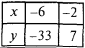
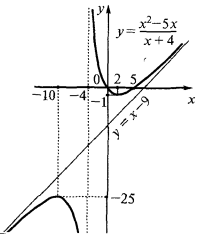


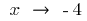 слева
слева 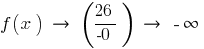
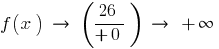
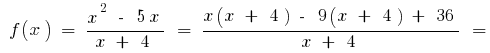
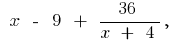 то при
то при 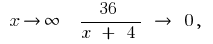 тогда
тогда 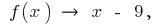 т. е.
т. е. 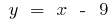 — наклонная асимптота
— наклонная асимптота