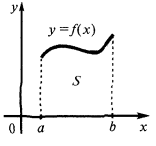
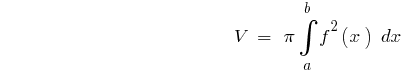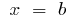Площадь криволинейной трапеции
Площадь криволинейной трапеции, ограниченной графиком непрерывной положительной на отрезке 
функции,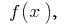 
осью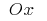 
и прямыми 
и 
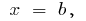равен
Пример.Вычислить площадь фигуры, ограниченной линиями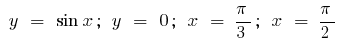 
Изображая эти линии, получаем криволинейную трапецию
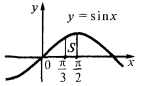
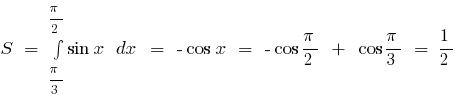
Площадь фигуры ограниченной графиками двух функций и прямыми 
и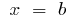 
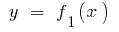Если на заданном отрезке непрерывные функции 
и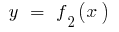 
имеют то свойство, что 
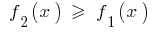для всех 
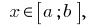то
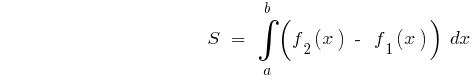
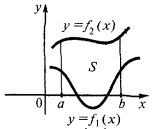
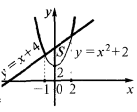
Пример.Вычислить площадь фигуры, ограниченной линиями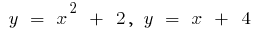 
Изобразим заданные линии и абсциссы их точек пересечения.
Абсциссы точек пересечения: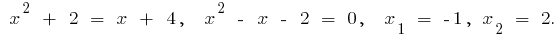 
Тогда по формуле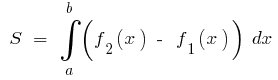 
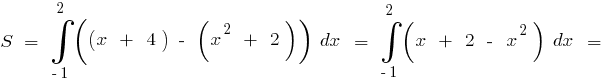
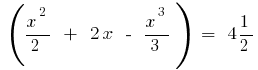
Объемы тел
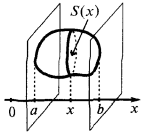
В общем случае
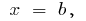Если тело заключено между двумя перпендикулярными к оси плоскостями, проходящими через точки и то
где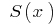 
— площадь сечения тела плоскостью, которая проходит через точку 
и перпендикулярна к оси
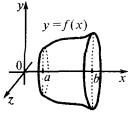
Для тела вращения
Если тело получено в результате вращения вокруг оси 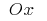криволинейной трапеции, которая ограничена графиком непрерывной и невідємної функции 
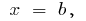на отрезке и прямыми и то
